2011. 3. 12. 15:27 Daily lives
최근 읽는 책과 그 단상
 |
맹자 교양강의 푸페이룽 지음, 정광훈 옮김/돌베개 |
 |
한비자 송지영/홍신문화사 |
'Daily lives' 카테고리의 다른 글
| 근황 (2) | 2011.07.09 |
|---|---|
| 시간을 따라 흘러간다는 것 (0) | 2011.06.06 |
| 짧게 잡소리 (2) | 2011.01.08 |
| 근황 (4) | 2010.12.18 |
| 근황 (2) | 2010.10.22 |
2011. 3. 12. 15:27 Daily lives
 |
맹자 교양강의 푸페이룽 지음, 정광훈 옮김/돌베개 |
 |
한비자 송지영/홍신문화사 |
| 근황 (2) | 2011.07.09 |
|---|---|
| 시간을 따라 흘러간다는 것 (0) | 2011.06.06 |
| 짧게 잡소리 (2) | 2011.01.08 |
| 근황 (4) | 2010.12.18 |
| 근황 (2) | 2010.10.22 |
2011. 3. 12. 14:19 Report/Books
 |
영단어 인문학 산책 -  이택광 지음/난장이 |
| 이영도, [그림자 자국] (0) | 2011.04.09 |
|---|---|
| Nassim Nicholas Taleb, [블랙 스완] The Black Swan (0) | 2011.03.15 |
| 이어령, [젊음의 탄생] (0) | 2011.01.29 |
| 진중권, [미학 오디세이] 시리즈 (0) | 2010.10.11 |
| 크로스로드 SF 단편집, 『죽은 자들에게 고하라』 (2) | 2010.06.27 |
2011. 1. 29. 22:19 Report/Books
 |
젊음의 탄생 (반양장) -  이어령 지음/생각의나무 |
| Nassim Nicholas Taleb, [블랙 스완] The Black Swan (0) | 2011.03.15 |
|---|---|
| 이택광, [영단어 인문학 산책] (0) | 2011.03.12 |
| 진중권, [미학 오디세이] 시리즈 (0) | 2010.10.11 |
| 크로스로드 SF 단편집, 『죽은 자들에게 고하라』 (2) | 2010.06.27 |
| 틸 바스티안, [가공된 신화, 인간] (2) | 2010.05.08 |
2011. 1. 29. 13:37 Mathematics/Quiz
| 기하 퀴즈 하나 (2) | 2010.04.30 |
|---|---|
| 월급을 황금 막대기로 주기 (4) | 2010.03.08 |
2011. 1. 16. 17:40 Mathematics
\text{To find the maximum of }G=G(x_1,\cdots,x_n)\\\text{Find }(\chi_1,\cdots,\chi_n) \text{ where } \nabla G=0\text{But }R=R(x_1,\cdots,x_n)\text{must satisfy the relation }R=0\text{To handle the problem, let }n=2\\\text{The exact differential of }R \text{ becomes}\\dR=\frac{\partial R}{\partial x_1}dx_1+\frac{\partial R}{\partial x_2}dx_2\\\text{when infinitesimal movement does not violate the requirement;}\\dR=0\text{When the function }G\text{ takes the extremum at the point}\\\text{The exact differential of }G \text{ also satisfies}\\dG=\frac{\partial G}{\partial x_1}dx_1+\frac{\partial G}{\partial x_2}dx_2=0\\\text{under the condition that }dR=0
\frac{\partial R}{\partial x_1}dx_1+\frac{\partial R}{\partial x_2}dx_2=0\\\therefore dx_1=-\frac{\frac{\partial R}{\partial x_2}}{\frac{\partial R}{\partial x_1}}dx_2\\\therefore dG=\frac{\partial G}{\partial x_1}dx_1+\frac{\partial G}{\partial x_2}dx_2\\=\left[-\frac{\partial G}{\partial x_1}\frac{\frac{\partial R}{\partial x_2}}{\frac{\partial R}{\partial x_1}}+\frac{\partial G}{\partial x_2}\right]dx_2\\=0\\\text{However, we are free to choose } dx_2 \text{, which implies}\\-\frac{\partial G}{\partial x_1}\frac{\frac{\partial R}{\partial x_2}}{\frac{\partial R}{\partial x_1}}+\frac{\partial G}{\partial x_2}=0
dR=0, dG=0\\\therefore dR-\alpha dG\\=\left[\frac{\partial R}{\partial x_1}-\alpha\frac{\partial G}{\partial x_1}\right]dx_1\\+\left[\frac{\partial R}{\partial x_2}-\alpha\frac{\partial G}{\partial x_2}\right]dx_2\\=0\text{However, as the restriction is still not removed,}\\\frac{\partial R}{\partial x_1}dx_1+\frac{\partial R}{\partial x_2}dx_2=0\\\therefore dx_1=-\frac{\frac{\partial R}{\partial x_2}}{\frac{\partial R}{\partial x_1}}dx_2
\text{Therefore under this restriction, we can freely choose }dx_2\\\frac{\partial R}{\partial x_1}dx_1+\frac{\partial R}{\partial x_2}dx_2=0
\text{Assume we choose }\alpha\text{ so that}\\\frac{\partial R}{\partial x_1}-\alpha\frac{\partial G}{\partial x_1}=0\\\text{Then }dR-\alpha dG =0 \text{ reduces to}\\\left[\frac{\partial R}{\partial x_2}-\alpha\frac{\partial G}{\partial x_2}\right]dx_2=0\\\text{As we are free to choose }dx_2 \text{, we must conclude that}\\\frac{\partial R}{\partial x_2}-\alpha\frac{\partial G}{\partial x_2}\text{ must be zero as well}
| 개드립의 마지막 정리 (0) | 2013.10.29 |
|---|---|
| 델타 분포 만들기 (6) | 2012.08.23 |
| 경계조건의 중요성 - Boundary condition (2) | 2010.08.21 |
| Involute 곡선 (10) | 2010.05.01 |
| 수학의 아름다움 (2) | 2010.04.24 |
2011. 1. 8. 14:23 Daily lives
 |
한비자 송지영/홍신문화사 |
| 시간을 따라 흘러간다는 것 (0) | 2011.06.06 |
|---|---|
| 최근 읽는 책과 그 단상 (0) | 2011.03.12 |
| 근황 (4) | 2010.12.18 |
| 근황 (2) | 2010.10.22 |
| Big Bang Big Boom (2) | 2010.07.16 |
2010. 12. 18. 12:43 Daily lives
 |
역사란 무엇인가 E.H. 카 지음, 김택현 옮김/까치글방 |
| 최근 읽는 책과 그 단상 (0) | 2011.03.12 |
|---|---|
| 짧게 잡소리 (2) | 2011.01.08 |
| 근황 (2) | 2010.10.22 |
| Big Bang Big Boom (2) | 2010.07.16 |
| 책 취향 (2) | 2010.07.09 |
2010. 11. 22. 13:30 Physics/Concepts
2010/08/03 - 엔트로피 - 고전적인 정의
1. 카르노 기관을 뛰어넘는 효율을 갖는 기관은 없다.
2. 이상적인 과정만 존재하는 경우에는
∮(δQT)ideal=0
이 성립하고, 그 값을 엔트로피의 변화량이라 정의할 수 있다.
| Dirac Equation(1) (4) | 2013.12.15 |
|---|---|
| 볼츠만 분포 (0) | 2013.09.20 |
| 엔트로피 - 고전적인 정의 (7) | 2010.08.03 |
| Hamiltonian formulation(1) (4) | 2010.07.14 |
| Contravariant/Covariant/Metric tensor와 Kronecker delta (2) | 2010.02.28 |
2010. 11. 1. 12:00 Knowl
| 행운의 여신은 뒷머리가 없다? (0) | 2013.08.29 |
|---|---|
| Theo Jansen의 Kinetic Sculptures - 덤으로 Walking mechanism까지 (4) | 2012.02.13 |
| 란체스터 법칙 (2) | 2010.09.30 |
| 에릭 호퍼 - 광신도의 반대는... (0) | 2009.05.15 |
| 금속가격 (4) | 2009.05.13 |
2010. 10. 23. 13:00 Physics/Special




| 그 많던 종이비행기는 어떻게 다 날았을까 (8) | 2013.10.06 |
|---|---|
| 자기 단극자의 vector potential (0) | 2011.10.03 |
| [물벽깨-2] 동시성의 상대성이란 무엇인가 - 실체진실의 장 1에대한 반론 (16) | 2009.01.08 |
| [물벽깨-1] 특수상대론은 무엇인가 (10) | 2008.12.01 |
| 특별기획 - 물리의 벽을 깨라! (6) | 2008.11.20 |
2010. 10. 22. 18:34 Daily lives
| 짧게 잡소리 (2) | 2011.01.08 |
|---|---|
| 근황 (4) | 2010.12.18 |
| Big Bang Big Boom (2) | 2010.07.16 |
| 책 취향 (2) | 2010.07.09 |
| 트위터나 해볼까 (0) | 2010.06.27 |
2010. 10. 11. 13:30 Report/Books
 |
미학 오디세이 3권 세트 -  진중권 지음/휴머니스트 |

 |
미학 오디세이 1 진중권 지음/휴머니스트 |

 |
미학 오디세이 2 진중권 지음/휴머니스트 |
 |
트로이 아델 게라 지음, 강경화 옮김/열림원 |
 |
미학 오디세이 3 진중권 지음/휴머니스트 |
| 이택광, [영단어 인문학 산책] (0) | 2011.03.12 |
|---|---|
| 이어령, [젊음의 탄생] (0) | 2011.01.29 |
| 크로스로드 SF 단편집, 『죽은 자들에게 고하라』 (2) | 2010.06.27 |
| 틸 바스티안, [가공된 신화, 인간] (2) | 2010.05.08 |
| 아스트랄한 맛이 일품인 철학 입문서, [철학에는 유머가 없는가] (0) | 2009.10.25 |
| Theo Jansen의 Kinetic Sculptures - 덤으로 Walking mechanism까지 (4) | 2012.02.13 |
|---|---|
| 골드버그 장치(Rube Goldberg Machine) (6) | 2010.11.01 |
| 에릭 호퍼 - 광신도의 반대는... (0) | 2009.05.15 |
| 금속가격 (4) | 2009.05.13 |
| 국가가 강요하더라도 양심에 반하는 짓은 절대 하지 말아라 - A. Einstein (10) | 2009.01.21 |
2010. 9. 20. 13:00 Physics/Speculations
\left< b | a \right>_{\text{in } \bold A}=\left< b |a\right>_{\bold A=0}\cdot\exp\left[\frac{iq}{\hbar}\int_a^b\bold A\cdot d\bold s\right]L=\sum_j\frac1{2}m\dot{x_j}^2-q(\varphi-\dot{x_j}A_j)=\frac1{2}m\vec{v}\cdot\vec{v}-q(\varphi-\vec{v}\cdot\vec{A})
p_i=\frac{\partial L}{\partial\dot {x_i}}=m\dot{x_i}+qA_iH= \sum_i p_i\dot{x_i}-L=\sum_i\frac12m\dot{x_i}^2+q\varphi\dot{x_i}=\frac{p_i-qA_i}m
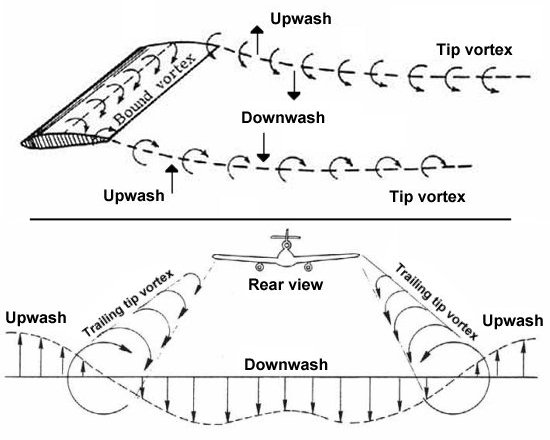
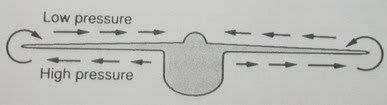
\\\therefore H=\sum_i\frac1{2m}(p_i-qA_i)^2+q\varphiH=\frac1{2m}(-i\hbar\vec\nabla-q\bold A)\cdot(-i\hbar\vec\nabla-q\bold A)+q\varphiH=-\frac{\hbar^2}{2m}(\vec\nabla-\frac{iq}{\hbar}\bold A)\cdot(\vec\nabla-\frac{iq}{\hbar}\bold A)+q\varphi\left(\frac{d}{dx}-f(x)\right)g(x)~e^{F(x)}=g'(x)~e^{F(x)}\Psi(x,t)=\Psi_0(x,t)\cdot\exp\left[\frac{iq}{\hbar}\int_a^b\bold A\cdot d\bold s\right]i\hbar\frac{\partial\Psi}{\partial t}=H\Psi=\left[-\frac{\hbar^2}{2m}(\vec\nabla-\frac{iq}{\hbar}\bold A)\cdot(\vec\nabla-\frac{iq}{\hbar}\bold A)+q\varphi\right]\Psi \\=\exp\left[\frac{iq}{\hbar}\int_a^b\bold A\cdot d\bold s\right]\cdot\left[-\frac{\hbar^2}{2m}\nabla^2+q\varphi\right]\Psi_0 \\=i\hbar\frac{\partial}{\partial t}\left(\exp\left[\frac{iq}{\hbar}\int_a^b\bold A\cdot d\bold s\right]\cdot\Psi_0\right)i\hbar\frac{\partial\Psi_0}{\partial t}=\left[-\frac{\hbar^2}{2m}\nabla^2+q\varphi\right]\Psi_0| 학사졸업논문 - 자기 단극자 (0) | 2013.07.07 |
|---|---|
| 양자역학의 유래(2) (0) | 2012.11.08 |
| 어는점내림 상수 구하기, 보론 (0) | 2010.09.03 |
| Kutta-Joukowski Theorem, alternate proof(without residue theorem) (4) | 2010.05.30 |
| Thin airfoil theory의 결과물에 대해서(flat plate) (2) | 2010.04.24 |
2010. 9. 11. 13:00 Programme
| Reversible Computation (0) | 2013.10.29 |
|---|---|
| [C] Conway's Game of Life (4) | 2010.06.25 |
| [C] Pseudorandom number generator (0) | 2010.06.14 |
| C언어 달팽이(나선)배열 (7) | 2010.04.26 |
2010. 9. 3. 12:30 Physics/Speculations
| 양자역학의 유래(2) (0) | 2012.11.08 |
|---|---|
| Electromagnetism in Schrodinger Eqn. (1) | 2010.09.20 |
| Kutta-Joukowski Theorem, alternate proof(without residue theorem) (4) | 2010.05.30 |
| Thin airfoil theory의 결과물에 대해서(flat plate) (2) | 2010.04.24 |
| 양자역학의 유래 (4) | 2010.01.19 |
2010. 8. 21. 13:00 Mathematics
\nabla^2\theta can be zero everywhere inside the lump of metal is for \theta to be a constant. [...]f(x,y)=e^y\cos x\\\nabla^2f=\left(\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}\right)f=0\theta(\rho,\phi,z)= J_1(\rho)\cos\phi\cosh z\theta는 상태함수의 위상이라 그 절대적인 값은 의미가 없어 임의의 지점에 임의의 값을 대응시켜 주는 것은 자유롭지만 문제는 그 자유도는 한 점에 국한된다는 것이다. 다시 한번 말하면, 금속 표면의 한 점에서 위상을 0으로 주었다고 금속 표면 전체의 위상이 0이라는 근거는 없다. 나는 파인만씨가 다음 식(21.19)만 만족하면 되기에 게이지 자유도(gauge freedom)를 이용해 \theta를 벡터포텐셜 A로 흡수시켰다고 추측할 뿐이다.mv=\hbar\nabla\theta-q\bold A~~~~~~~~\text{(21.19)}| 델타 분포 만들기 (6) | 2012.08.23 |
|---|---|
| Lagrange Multipliers - 라그랑주 승수법 (7) | 2011.01.16 |
| Involute 곡선 (10) | 2010.05.01 |
| 수학의 아름다움 (2) | 2010.04.24 |
| Power set, again (0) | 2010.04.17 |
2010. 8. 11. 13:30 Writer
| 한글 본문, 영어 제목 (0) | 2011.08.28 |
|---|---|
| Luna venator (0) | 2011.06.04 |
| but a grin without a cat! (0) | 2010.04.10 |
| 새 물리 교과과정 (4) | 2010.04.09 |
| 로피탈과 한국문학 (2) | 2010.04.02 |
2010. 8. 3. 13:00 Physics/Concepts
2008/12/21 - 제레미 리프킨, 엔트로피
무질서도로 번역되는 엔트로피(Entropy)란 개념은 열역학 제 2법칙과 밀접한 관계를 갖습니다. 제 2법칙이 엔트로피 증가의 법칙으로 통용되는 것만 보아도 그것을 쉽게 알 수 있겠지요.
엔트로피에 대한 접근은 크게 두가지로 볼 수 있습니다.(정보 이론에서도 다룬다고 하는데 이건 무시.. 세스 로이드의 『프로그래밍 유니버스』란 책에서 간략하게 다루고 있는데 그걸 참고하셔도 좋을 듯 합니다.) 하나는 완전한 고전역학적인 접근이고 다른 하나는 완전한 통계역학적인 접근입니다. 고전역학적인 접근은 우리가 어느 물체에 대해 평균적인 값으로 측정하는 물리량(압력이나 부피, 밀도 등)을 기반으로 엔트로피를 정립해 나가는 것이고 통계역학적인 접근은 분자들의 상태의 수를 이용해서 엔트로피를 정립해 나가는 방식입니다. 보통은 통계역학적인 접근, 혹은 미시적인 접근을 주로 사용하지만 좀 독특한(일반적인 접근인 미시적인 접근과는 반대되는 접근이라는 점에서) 접근방식인 고전역학적인 접근을 써 보려고 합니다.1
먼저 카르노 기관(순환Cycle)을 짚고 넘어가야 합니다. 카르노 기관은 엔트로피라는 개념이 정립되기 전부터 등장해서 엔트로피를 고전적으로 정의하는데 커다란 버팀목이 되었던 가상적인 엔진입니다. 이 엔진의 특징은 '모든 과정이 역으로 진행 가능하다'입니다.
카르노 기관(Carnot engine/cycle)
모든 과정이 역행 가능한 기관. 네 단계로 구성된다.
1. 등온팽창. 엔진과 같은 온도를 가진 열 공급원에서 에너지를 흡수한다. 같은 온도를 갖기 때문에 이 과정은 역으로 동일하게 진행될 수 있다.
2. 단열팽창. 엔진은 외부와 열 교환을 할 수 없다. 이때 팽창은 준정적Quasi-static으로 일어난다. 준정적이란 말은 평형상태와 유사하게라는 뜻으로, 이 경우에는 기체(또는 유체working fluid)의 팽창이 내부의 압력과 외부의 압력이 동일한 상태에서 일어나는 것이다. 이렇게 준정적인 과정으로 기체가 팽창할 경우 과정은 역으로 진행될 수 있다.
3. 등온압축. 엔진과 같은 온도를 가진 열 흡수원에 에너지를 방출한다. 등온팽창과 마찬가지의 이유로 역으로 동일하게 진행될 수 있다.
4. 단열압축. 단열팽창과 마찬가지로 열 교환을 할 수 없으며, 마찬가지의 조건과 이유로 과정은 역으로 진행할 수 있다.
그리고 열역학 제 2법칙의 공리가 등장합니다. 두 가지 공리가 있습니다.2
Clausius Statement
열은 자연적으로 저온부에서 고온부로 전달될 수 없다.3
Kelvin-Plank Statement
단일열원에서 열을 얻어 모두 일로 바꾸는 것은 불가능하다.
살펴보겠지만, 두 공리는 서로 동등한 관계를 지닙니다. 둘 중 하나만 부정되어도 다른 하나마저 부정되어야 하지요. 먼저 첫 서술을 부정해 보겠습니다. 열이 자동적으로 저온에서 고온으로 이동하는 겁니다. 그러면 어떤 순환이 두 열원 사이에서 작동하면서 저온부에 버리는 열이 고온으로 이동하면 외부에서 보기에는 고온에서 얻은 열을 전부 일로 바꾼 것으로 보이게 됩니다. 둘 째 서술이 부정되는 것이지요.
둘 째 서술을 부정해 볼까요? 단일열원에서 열을 얻어 모두 일로 바꾸는 기관을 냉동기에 연결합니다. 그러면 저온부에서 고온부로 스스로 이동하는 현상이 일어나게 됩니다. 첫 서술이 부정되는 겁니다. 결국 서로 동치라고 볼 수 있겠지요.
뭐 어찌되었든, 이를 이용하면 카르노 기관이 최고의 효율을 가진 기관이라는 것을 보일 수 있습니다. 카르노 기관은 기본적으로 외부에 영향을 미치지 않는 기관입니다. 모든 과정을 그대로 역으로 진행할 수 있기 때문이지요. 하지만 이 기관보다 효율이 좋은 기관을 도입한다면? 이런 이상적인 기관에서 일을 얻어서 카르노 기관을 역으로 진행시키는 데 사용한다면 열이 역류하는 현상이 일어납니다. 이는 Clausius의 서술에 위배되기 때문에 결국 그런 기관은 존재할 수 없다는 것이지요.
그리고 동일한 열원 사이에서 작동하는 카르노 기관들은 전부 같은 효율을 지닙니다. 하나가 다른 하나보다 더 효율이 좋으면, 하나를 냉동기로 사용하고 하나를 냉동기를 작동시키는 엔진으로 사용하면 열이 역류하는 현상을 볼 수 있겠지요. 이 역시 Clausius의 서술과 반대되기 때문에 존재할 수 없습니다.
그러면 같은 열원이란 무엇일까요? 동일한 온도를 가진 열원을 같은 열원이라고 말합니다. 그리고 카르노 기관의 효율은 그 기관이 작동하는 두 열원의 온도의 함수로 주어집니다. 이는 고온부와 저온부 그리고 그 사이에 중간단계의 열원이 존재함을 가정하고 고온부와 저온부 사이에서 작동하는 기관 하나, 고온부와 중간단계 사이에서 작용하는 기관 하나, 중간단계와 저온부 사이에서 작동하는 기관 하나를 놓은 다음 고온부에서 바로 저온부로 연결된 기관과 중간단계를 걸처 작동하는 기관 둘의 합이 같은 효율을 가져야 한다는 것을 이용해서 보일 수 있습니다.4 고온부의 온도를 th, 저온부의 온도를 tl, 중간 단계의 온도를 tm이라고 한다면 저온부와 고온부 사이 그러니까 th와 tl 사이에서 작동하는 카르노 기관의 효율은 이런 꼴로 나타날 것입니다.
ηhl=F(th,tl)=1−QlQh
Q는 카르노 기관에서 들어오거나 나가는 열의 양을 말하고, 첨자는 그 온도를 말합니다. 앞으로는 편의상 열을 주고받는 비율에 초점을 맞추겠습니다. 이 열을 주고받는 비율은 다음과 같이 식의 형태로 쓸 수 있지요.
QlQh=f(th,tl)
중간 단계에 걸쳐있는 나머지 두 카르노 기관에 대해서도 같은 식을 써 볼 수 있습니다.
QhQm=f(th,tm)QmQh=f(tm,tl)
그리고 효율이 같다는 것에서 다음 식을 유도할 수 있습니다.
ηhl=1−QlQh=ηh|m|l=1−QhQmQmQlQlQh=QhQmQmQl∴f(th,tl)=f(th,tm)f(tm,tl)
마지막 식을 다음과 같이 정리할 수 있는데
f(th,tl)f(tm,tl)=f(th,tm)
이렇게 되면 좌변에서만 tl이 등장하므로, f는 변수분리가 가능한 함수가 됨을 알 수 있습니다. tl만 변화했을 때 값이 변해서는 안 되기 때문에 분모인 함수가 tl에 의해 받는 영향만큼 분자의 함수가 영향받아야 되기 때문이죠. 그러면 일단 함수를 나눈 다음 생각해 봅시다. 함수 f를 대충 분리해서
f(t1,t2)=ϕ(t1)θ(t2)
라고 둔다면
f(th,tm)=ϕ(th)ϕ(tm)
을 얻게 되지요. 그런데 우리는 온도의 측정에 제한을 둔 적이 없기 때문에 함수 ϕ를 온도를 정의하는데 사용할 수도 있습니다. 이를 열역학적 온도라고 부릅니다.
T=ϕ(t)
이제 열역학적 온도를 이용해 카르노 기관의 열효율을 정의할 수 있게 됩니다.
ηhl=1−TlTh=1−QlQh
물론 이를 이용해 기준온도를 두고5 다른 열역학적 온도를 측정하는 것도 가능하지요. 위의 식에서 흡수/방출하는 열이 온도와 정확히 비례하기 때문입니다.
T2=Q2Q1 T1
이제 엔트로피를 도입할 수 있게 됩니다. 먼저 다음 값을 한번의 카르노 순환(cycle)에 대해서 계산해 봅시다.
∮δQT
이때 Q는 계 안으로 흘러들어오는 열로 정의합니다. 단열과정에서는 열이 전혀 흐르지 않기 때문에 등온과정만 생각하면 되는데, 등온과정에서 T는 일정하므로 적분은 다음과 같습니다.
∮δQT=QhTh+−QlTl
(두번째 항에 음의 부호가 붙어있는 이유는 저온부로 열이 방출되기 때문입니다.) 그런데 위에서 카르노 기관의 등온과정에서 흡수하거나 방출하는 열은 온도에 비례한다고 정의내렸었죠.6 따라서 저 값은 영이 됩니다.
Q∝T∴∮δQT=QhTh−QlTl=0
더군다나 어떤 열역학적인 기구라고 하더라도 이상적으로만 작동하고 원래대로 돌아오는 주기운동을 하는 경우라면 수많은 작은 카르노 기관을 모아 만들 수 있습니다. 그러므로 이상적인 경우만 존재한다면 다음 결론을 얻습니다.
∮(δQT)ideal=0
다른 뜻으로는, 위 미분값이 완전미분이라는 것이지요. 완전미분량이기 때문에 위 미분을 어떤 스칼라 함수의 미분으로 볼 수 있다는 것입니다. 스칼라 함수라면 상태에 의존하는 값이라는 의미고, 그러므로 상태에만 의존하는 이 스칼라 함수를 하나의 물리량으로 볼 수 있다는 뜻입니다. 이 물리량이 바로 엔트로피입니다. 대신 엔트로피의 차이만 정의되지 엔트로피의 절대값은 정의되지 않습니다. 위치에너지와 비슷하지요.7
(δQT)ideal=dS∴∮dS=0
통계역학 이전의 열물리에서 엔트로피라는 물리량이 어떻게 얻어졌는지를 보이는 것은 끝났고, 열역학 제 2법칙의 또 다른 버젼인 '엔트로피는 계속 생성된다'는 다음에 다루어 보도록 하죠. 스포일러: 이건 어떤 순환이라고 하더라도 이상적인 경우보다 효율이 떨어진다는 사실을 이용해 증명합니다.
많이 오래 전에 쓰다 만 글이라 문체가 조금 다릅니다. 별로 상관없지만...-.-;;
| 볼츠만 분포 (0) | 2013.09.20 |
|---|---|
| 열역학 제 2 법칙과 엔트로피 증가의 법칙 (3) | 2010.11.22 |
| Hamiltonian formulation(1) (4) | 2010.07.14 |
| Contravariant/Covariant/Metric tensor와 Kronecker delta (2) | 2010.02.28 |
| 자기 단극자, Dirac String, 기타 등등 (0) | 2010.01.01 |
2010. 7. 24. 12:33 Writer/Short
그래서 그게 이야기의 끝이야? 나태(懶怠)가 묻는다. 다언(多言)이 대답한다. 끝이야. 잠자코 있던 탐욕(貪慾)이 고개를 든다. 뭐야. 너답지 않게 이야기가 너무 단순한 것 같은데? 그런가? 내 나름대로는 다채로운 이야기였다고 생각하는데. 너라면 무언가 더 끄집어낼 줄 알았지. 탐욕의 말이 끝나자 나태가 다시 말을 꺼낸다. 교만(驕慢), 너가 한번 이야기해봐라. 다언이 거든다. 그래, 너 이야기 하나는 멋지게 하잖아. 잠깐의 침묵. 그리고 교만이 입을 연다. 그렇다면 내가 너희들에게 최고의 이야기를 선사해주지. 교만은 점차 비대해지더니 모두를 집어삼킨다. 낮을 덮치는 어둠과도 같이. 그리고 이야기는 시작된다. 어둠의 소용돌이 속에서.
태초에 말이 있었다.
"빛이 있으라."
말은 힘이요, 언어는 권력이었다. 자신으로부터 자라난 세계가 모태를 삼키리라는 것을 모르는 듯 말은 세계의 이것저것을 빚어내었다. 빛을 모아 낮을 만들자 어둠은 모여 밤이 되었고, 부스러기를 긁어모아 땅을 만들자 남은 먼지는 모여 바다가 되었다. 이 모든 것이 아직 말에게 힘이 있었던 시대의 일이다.
간이 플라스틱 의자가 불편해질 즈음이었다.