Dexter's story

Thin airfoil theory는 말 그대로 날개가 얇다고 가정을 한 상태에서 날개 주변의 유동에 대해 해석적인(analytic) 해를 구하는 것이다. 상당히 극단적인 가정이 많이 들어가기는 하지만 의외로 잘 맞아서(실험 데이터와 오차범위를 비교해놓은 것을 보면 정확하다는 말만 나온다.) 이전에 공학과 흑묘백묘론이라는 글을 쓰는 모티브가 되기도 했다. 물론 모티브는 내 엉망인 글 솜씨에 의해서 망해버렸지만.

근사를 하는 과정은 다음과 같다.

1. 점성항을 제거한다.
Navier-Stokes 공식을 Euler 공식으로 바꾸는 것이다. 이렇게 공식을 바꾸어주면 그나마 풀 수 있는 문제로 바뀌게 된다.^[각주:1]

2. 회전하지 않는다고 가정한다.
속도 벡터장의 회전도(curl)를 항등적으로 0으로 취급한다는 뜻이다. 1번과 함께 이 조건이 만족되면 속도를 스칼라 함수의 물매(gradient)로 쓸 수 있다고 해서 potential flow라고 부른다. 컴퓨터 없이 유체역학을 공부하게 되면 이런 종류의 흐름만 배울 것이다.

3. 날개를 camber만 남긴다.
camber는 날개의 윗 단면과 날개의 아랫 단면의 정중앙을 지나는 곡선이다. 임의의 수직선을 생각했을 때 camber가 날개를 정확히 반으로 가른다고 생각해도 좋고, 윗 단면과 아랫 단면의 평균이라고 생각해도 좋다. 중요한 것은 날개에 이 녀석만 남겨서 두께를 0으로 만들어 버린다는 것이다.

4. x축에 vortex를 적절히 배치한다.^[각주:2]
말 그대로 적절히 배치한다. 이 배치를 잘 조절해서 camber만 남긴 날개와 유체의 흐름이 평행하도록 만들어주는 것이다. 비행기가 날 때 공기가 날개를 뚫고 흐르지는 않는 것을 모사한다.

정확한 것은 책을 찾아보세요. 블로그는 언제까지나 블로그이다.

문제는 결국 이 방정식으로 줄어들게 된다. gamma는 x축 위의 vortex 분포, V는 무한지점에서 불어오는 속도(그래서 아래첨자가 무한대이다), alpha는 받음각(angle of attack), x는 좌표, z는 camber의 공식. 0에서부터 c까지 적분한다는 소리는 날개의 앞쪽 끝에서 뒤쪽 끝까지 적분한다는 의미이다.


Anderson의 Fundamentals of Aerodynamics 4th Ed.을 쓰고 있는데, 여기서는 날개를 완전히 평평한 판으로 근사했을 때(dz/dx=0)의 해를 다음과 같이 구해놓았다.


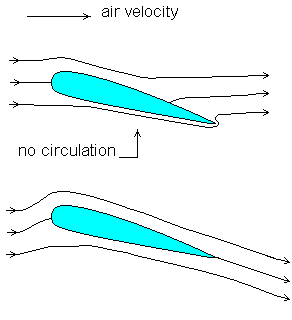
재미있는 것은 이 식이 경험법칙인 Kutta condition을 만족한다는 사실이다. Kutta 조건은 어떤 실험을 해 보아도 날개 끝 지점에서 유체의 움직임은 끝의 생김새와 평행하다는 것이다. 수식으로 바꾸면 gamma가 날개의 끝 지점에서는 0이라는 말이다.


아래 그림이 Kutta 조건을 만족할 때의 유동 모습이다. 일단 책에 나온 해의 그래프는 다음과 같이 그려진다.


자, 어떻게 다음 적분방정식(integral equation)의 해가 저렇게 깔끔한 성질을 보여줄까?


결론부터 말하자면, 당연히 깔끔할 수 밖에 없다. 일반적으로 적분방정식의 해는 여러개가 나오는데 그 중에서 우리가 원하는 조건에 맞는 녀석만 남도록 경계조건(boundary condition)을 적용했기 때문이다.^[각주:3] 방정식 자체는 alpha와 V의 부호를 동시에 바꾸어도 동일하다는 점에 주목하길 바란다. 이 말은 위에서 구한 분포가 반대 방향에서 불어오고 있을 때에도 유효한 답이 된다는 말과 똑같은 소리이다.

다르게 표현한다면 다음 해도 사실은 유효하다는 것이다.부호 반대.

\gamma(\theta)=2\alpha V_\infty\frac{\cos(\theta)-1}{\sin(\theta)}\\x=\frac{c}2(1-\cos(\theta))