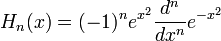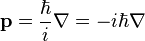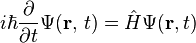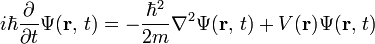양자역학에서 가장 유명한 commutator를 뽑으라면 누구나 하이젠베르크의 불확정성 원리를 꼽을 것이다. 아무래도 제일 먼저 발견된 교환이 불가능한 물리량이니까.
[x,p]=xp-px=i\hbar
그런데 왜 i가 붙을까? 고민해본 사람? 문제는 의외로 쉽게 풀린다. 두 측정가능한 물리량 A와 B를 가정하자. 따라서 A와 B는 에르미트(Hermitian) 연산자이다. 적당한 양자책을 잘 공부했다면 이를 설명할 필요는 없을 터(간단하게 말하자면 고유값(eigenvalue)이 실수가 나와야 해서). 한번 유도해보자.
\text{For observables }A,B\\A^\dagger=A, B^\dagger=B \\\\\therefore [A,B]^\dagger=(AB-BA)^\dagger\\=B^\dagger A^\dagger-A^\dagger B^\dagger=BA-AB \\\\\therefore [A,B]^\dagger=-[A,B] \\\\\text{or, equivalently;} \\\exists C(C^\dagger=C),\,\,[A,B]=iC
측정 가능한 물리량의 commutator는 항상 반에르미트(anti-Hermitian) 연산자여야 한다는 결론을 얻는다. 반에르미트 연산자는 단위허수 i를 곱하거나 나눠서 에르미트 연산자로 만들어줄 수 있으니 이제 그 미스테리한 i가 어디에서 튀어나왔는지 알 수 있다.
이제 조금 더 재미있는 명제를 도출해보자.
\text{Assume observables }A,B\text{ and an eigenstate of }A\\\\A\left|a \right \rangle=a\left|a \right \rangle \\\\\text{Then, we get the expectation value of the commutator}\\\\ \left\langle a|[A,B]|a \right\rangle=\left\langle a|AB-BA|a \right\rangle = (a^\ast - a)\left\langle a|B|a \right\rangle=0
\\\\\text{or, equivalently;} \\\\ C \equiv \frac1i [A,B],\;A\left|a \right \rangle=a\left|a \right\rangle \Rightarrow\left\langle a|C|a \right\rangle=0 \\\\\text{for any observables }A, B
아직 이상한 점을 눈치 못챘는가? A에 x를, B에 p를 넣어보자.
[x,p]=i\hbar\\\\\therefore \left\langle x\middle|\frac1i[x,p]\middle|x \right\rangle=\hbar\left\langle x|x \right\rangle=0\\\left\langle p\middle|\frac1i[x,p]\middle|p \right\rangle=\hbar\left\langle p|p \right\rangle=0
?!?!
이 비정합성은 commutator가 identity의 배수이기 때문에 나타난다. 다르게 말한다면, 어떤 한 측정량이 다른 측정량과 만드는 commutator가 identity의 배수로 나온다면 그 측정량의 고유상태(eigenstate)는 그다지 예쁜 성질을 갖지 않으며(예컨데 위치 x의 고유상태나 운동량 p의 고유상태는 L2(Square-integrable)공간에 속하지 않는다), 따라서 주의를 기울여 다루어야 한다고 결론지을 수 있다.
참고로 가장 간단(?)한 양자화 방법은 고전역학에서의 Poisson bracket을 양자역학의 commutator로 해석하는 것이기 때문에(Dirac quantisation 혹은 canonical quantisation) 양자역학의 미래가 골치아프다는 것은 확실해졌다. 양자장론이 괜히 머리 뽀개지는게 아니라니까...
'Physics > Speculations' 카테고리의 다른 글
| Understanding de Sitter and Anti-de Sitter space (0) | 2015.08.25 |
|---|---|
| 일반상대론에서의 쌍둥이 역설 (0) | 2015.01.09 |
| Constraints on Commutators (5) | 2014.05.22 |
| 슈퍼맨은 팬티 위에 쫄쫄이를 입지 않아 (0) | 2014.01.15 |
| 광양자 가설 없이 어디까지 갈 수 있을까? (0) | 2013.12.04 |
| 레이저로 가열할 수 있는 최대 온도에 대하여 (1) | 2013.10.18 |
댓글을 달아 주세요
0 \times delta(0) = ? 문제랑 비슷하군요.
2014.05.23 00:05 신고함수 x\delta(x)로 읽어서 순간 당황했네요. 이 함수는 0이었죠(...)
아하 그런문제도. 더 간단하게는 0 * 무한대(infinity) 문제랑 비슷하겠네요 =ㅇ=;;ㅋ
(a-a)*<a|B|a> 에서 이게 0이라고 넘어갈때 이런문제가... <a|B|a>가 L2 (Square-integrable) basis 를 쓰는 경우가 아니라면 무한대도 될 수 있어서.
아무튼 생각지 못했던 부분이네요. 그런데 이게 "commutator가 identity의 배수이기 때문"이 맞나요? 그냥 state가 L2로 표기 안되어서 그런것도 같은데... 저것 때문이라고 단순히 말하면 필요/충분조건 요런거에서 헷갈리는 말인거 같아요. 양쪽 state가 L2로만 표현되면 그냥 숫자로 바꿀수 있긴 할테니까요.
양쪽의 state가 L2공간에 속한다고 하면 더 문제가 되겠죠. 우변이 0이니까 좌변 또한 0이어야 한다는 결론이 나오는건데, square-integrable하면 우변이 0*(유한한 숫자)가 되어서 빼도박도 못하는 0이 되어버리니까요. 관측가능량의 commutator로 identity가 나오는 순간 관련 고유상태의 규격화(normalisation)에 문제가 생긴다고 보는 편이 맞는 것 같습니다.
처음부터 A, B에 x,p를 넣고 전개해보면...
Then, we get the expectation value of the commutator
<x|[x,p]|x> = (x^* - x) <x|p|x> = ? (0 곱하기 무한대 형태라 결론을 못내림.)
여기서 ?가 '0' 이란 결론을 못내릴거란 이야기였는데...
그렇기 때문에
C \equiv [x,p]/i 라고 해도 => <x|C|x> = ? (위의 물음표와 같은 놈.)
란 결론까지 밖에 안되지 않나요? 뭔가 다른 이야기인가;;;;
x가 L2였다면야 <x|p|x>가 유한할테니 ?=0이라고 결론 내릴 수 있고. (있나??? p의 eigenvalue 중에 무한대가 있으면 이렇게 결론 내릴 수 없을수도 있는건가 =ㅇ=;;)
[x,p]가 identity의 배수라고 할지라도 (\equiv c) => <x|c|x>=0 이란 결론이?
아 이게 문제였구나;;; 제 이해가 뭔가 꼬였었네요.
결론적으론 L2 Hermitian operator A,B의 commutator [A,B]는 indentity의 배수가 될 수 없다가 되겠네요. 신기하넹 -ㅇ-;;; (지금 제가 이해한것도 듬성듬성 논리가 뚫려있어서 천천히 다시 생각해보긴 해야겠네요.)