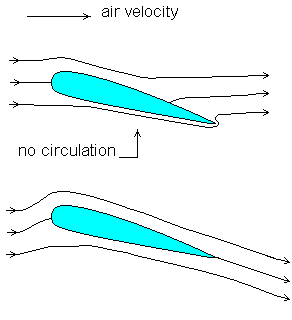
항공역학(사실상 유체역학이다만)을 배우다 보니 꽤 간단하면서도 중요한 식들을 보게 되는데, 그중 단연 으뜸이라고 할 수 있는 녀석은 이 녀석이다.
Kutta-Joukowski Theorem
L'=\rho_{\infty}V_{\infty}\Gamma
대문자 감마(Gamma)는
circulation이라고 불리는 녀석인데, 여기서는 이렇게 정의한다.
\Gamma=-\oint\vec V\cdot d\vec s
2차원 유동을 다룰 때 나오는 식이다. 예상하겠지만, circulation은 어떤 폐곡선을 따라 적분하느냐에 따라 값이 휙휙 뒤바뀐다. 그리고 전자기학 공부 조금이라도 깊게 한 사람은 알겠지만,
Stokes정리에 의해 대문자 감마를 다른 방식으로 구할 수 있다.
\Gamma=-\oint\vec V\cdot d\vec s~~~~~\\=-\int \vec\nabla\times\vec V dA
유체역학에서는 유동장 속도 벡터에 curl을 취한 벡터를
vorticity라고 부른다. 일반적으로 여기에 문자 하나를 배정해 주는데 크시(Xi)를 주로 쓰는 듯. 별로 중요하지는 않아 보이지만. 이 값은 그 위치에서 유동 성분이 어떤 각속도를 가지고 도는지를 나타낸다. 크시의 크기는 각속도의 두배.
\vec\xi=\vec\nabla\times\vec V
항공역학이다 보니 항공기에서 나타나는 유동을 주로 다루게 되는데, 일반적으로 vorticity는 0이다.(이러면 속도 벡터를 모함수의 물매(gradient)로 생각할 수 있어
potential flow라고 부른다.) 단순하게 생각해서 항공기가 앞으로 날아가면 항공기 입장에서는 공기가 앞에서 불어오는 것처럼 보인다. 그리고 앞에서 일정하게 불어오는 공기에게 각운동량 따위가 있을리가 없다. 어딘가를 중심으로 회전해야 각운동량이 생기기 때문이다. 뭐 일단 자세한 설명은 생략하고, 실제 물체가 있는 곳 주위를 제외한 다른 부분에서는 대부분 vorticity가 0이다. 이런 부분을 따라 contour를 그리는 것이다. 그런데 비행기가 뜨기 위해서는 lift가 존재해야 하고, 위의 정리를 따르면 circulation이 0이면 안된다. 그런데도 velocity potential 자체는 정의할 수 있다.
magnetic scalar potential과 비슷한 개념이라고 생각하면 될 듯 하다. 당연히 이 녀석은 Riemann surface 비슷하게 한 지점에서 하나의 값만 정의되지는 않는다. complex variable analysis에서 residue와 비슷하다고 해야 하나?
잡담은 여기까지 하고(무언가 헤맨 느낌이 들지만), 직접 증명해보자. 일반적으로는
complex potential을 이용한다고 하는데, 그런 고등한 방식은 우리에게 어울리지 않는다.(이 방법으로 증명한 것을 보고 싶으면
여기로) 좀 더 바로 바로 와 닿는 증명은 없을까? 구멍이 조금 있어 엄밀하지는 못하지만(메꿀 수는 있는 구멍이다.) 이런 방식으로 증명하는 것도 가능하다.
대충 다음처럼 airfoil 하나를 준다. Kutta조건을 만족하려면 아래처럼 흐르게 된다.
circulation이 생겼다. 그러면 이제 이 airfoil이 하나의 점처럼 보일 때까지 시야를 확대한다.

대충 이런 느낌이다.
이제 중요한 부분. 이렇게 매우 먼 지점에서 유체의 y방향 운동량 성분의 변화를 분석한다. 먼저 r이 매우 커지면 가장 중요한 성분은 다음 세 가지가 된다.
\text{at large } r\gg1\text{, flow field is characterized by}\\\\
\begin{array}{cc}
\text{flow from infinity}&V_\infty\hat x\\
\text{source flow}&\frac\Lambda{2\pi r}\hat r\\
\text{vortex flow}&-\frac\Gamma{2\pi r} \hat\theta
\end{array}\\\\
\text{on the first order of } \frac1r
r의 -1차항까지 분석하는 이유는 우리가 적분할 때 r의 order를 갖는 weighting factor를 부여할 것이기 때문이다. 일단 확실한 것은 airfoil이 있어도 유체가 새로 생성되거나 사라지지는 않는다는 것이다.
\Lambda=0
먼저 들어오는 y 운동량을 측정하자. 일단 다음과 같이 그림을 잡으면 미소시간 dt동안 들어온 y방향 성분을 알 수 있다.

a>>1으로 두기 때문에 위에서 얻은 근사식을 적용한다. 흘러 들어오는 질량은 수직길이당
\rho_\infty V_\infty dt 이므로 적분은 대충 다음처럼 생겼다.
p_{y,i}=\int_\infty^\infty \rho_\infty V_\infty dt\frac\Gamma{2\pi r}\cos\theta dl~~~~~~~~~~~~~~~~~\\
=\int_\infty^\infty \rho_\infty V_\infty dt\frac\Gamma{2\pi a\sec\theta}\cos\theta~ d(a\tan\theta)\\
=\int_{-\pi/2}^{\pi/2} \rho_\infty V_\infty dt\frac\Gamma{2\pi}d\theta\\
=\frac12\rho_\infty V_\infty \Gamma dt
뒷쪽에 대해서도 같은 식을 구할 수 있다. 다만 이 때는 vortex가 유도한 y성분의 속도 방향이 아래쪽이므로,
p_{y,o}=-\frac12\rho_\infty V_\infty dt
이다. 따라서 airfoil이 전체 유동장에 주는 힘은
\text{momentum transferred into the fluid flow} = p_{y,o}-p_{y,i}\\
=-\rho_\infty V_\infty\Gamma dt\\\\
\therefore \text{force transferred into the fluid flow}={p_{y,o}-p_{y,i}\over dt}\\
=-\rho_\infty V_\infty\Gamma
이제 뉴턴 3법칙을 이용한다.
\text{lift} = -\text{force transferred into the fluid flow}\\\\
\therefore L'=\rho_\infty V_\infty\Gamma~~~~~~~~~~~~~~~~~
증명 완료. 이런 방식으로 증명하게 되면 Navier-Stokes 방정식처럼 potential flow를 가정할 수 없는 경우에도 Kutta-Joukowski 정리가 대략적으로 성립한다는 것을 보여줄 수 있을지도 모른다는 생각이 들었지만 생각해보면 점성때문에 r의 -1차 항이 0으로 배는 빠르게 수렴하는구나. 교수님께서는 이 식이 점성이 있어도 대충 맞는다고 하셨는데 그렇게 잘 맞게 하려면 어떻게 contour를 잡는지에 대한 감각이 필요할 것 같다.
쓰고 나서 보니 막쓴 항들이 보이는데 너그러운 마음으로 무시해 주시길 바란다, 정 찝찝하면 dt를 Δt로 바꾸시면 되겠다.