Dexter's story

오늘 아카이브에 들어가봤다가 의외의 글을 발견했다.

http://arxiv.org/abs/1508.05607

de Sitter 공간에서 타키온을 올려놓은 문제인데, 사실 '어 이게 글로 나올 만한 문제였던가?'가 솔직한 감상. 고전적인 타키온 입자는 유한한 시간 동안만 생존한다는게 주요 내용인데(양자적인 경우는 조금 다르게 취급), '유한한 시간 동안 생존한다'는 해석을 빼면 전혀 새로울 것이 없었는지라. 다만 이런 느낌은 내가 타키온을 해석하는 방법 때문인지도 모르겠다.

우선 예전 글들 링크.

2015/01/09 - 일반상대론에서의 쌍둥이 역설

2014/01/11 - Poincare Half Plane 푸앙카레 반평면 (1)

2014/05/25 - Poincare Half Plane 푸앙카레 반평면 (2)

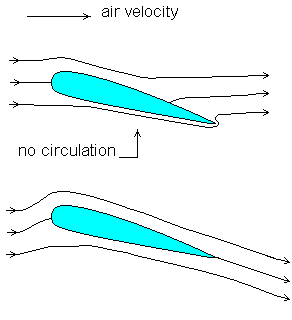
지금 보니 블로그에서 직접적으로 언급한 적이 없다는 것이 살짝 의외인데, de Sitter(이하 dS) 공간과 Anti-de Sitter(이하 AdS) 공간은 사실상 똑같은 공간이다. 푸앙카레 반평면 (1)글에서 마지막에 살짝 언급하고 넘어갔듯, 푸앙카레 반평면 (2)글에서 t와 z의 해석을 뒤바꿔주면 AdS 공간이 dS 공간으로 변한다. 이 말은 AdS 공간에 사는 질량이 있는 물질, 타디온(tardyon)들이 dS 공간의 질량 제곱이 음수인 물질, 타키온들과 똑같이 움직인다는 것을 의미한다. 그 반대로 dS 공간의 타디온들이 AdS 공간의 타키온들처럼 행동한다는 해석 또한 가능하고.

다만 우리가 일반적으로 생각하는 시공간에서는 시간 차원이 하나밖에 존재하지 않아서 완전히 동일하지는 않다. AdS/CFT에서와 같이 일반적으로 AdS 공간을 생각할 경우 한 차원 높은 민코프스키 공간에서 초쌍곡면을 그대로 가져다가 AdS 공간으로 잡지 않고 그 universal cover를 이용하곤 한다. 이 짓을 안 하면 closed timelike trajectory가 나와서 인과율에 문제가 생기기 때문이다. 이건 시간 방향이 1차원이라서 $S^1$의 위상을 갖기 때문에 가능한 일인데, 만약 시간 방향이 2차원이거나 보다 높은 차원을 가질 경우에는 $S^n$의 위상을 갖게 되고, $S^n$은 자기 자신이 universal cover이기 때문에 universal cover를 취해서 closed timelike trajectory를 없애는 것이 불가능해진다. n+1차원의 dS 공간에서 움직이는 타키온을 무작정 측지텐서의 부호를 뒤집어서 AdS 공간에서 움직이는 타디온으로 바꾸어 해석하려면 조심해야 할 필요가 있다는 소리.

여기까지는 주의사항이었으니 타키온에 물리적인 의미를 줄 수 있는 방법을 생각해보자. 일반상대론에서의 쌍둥이 역설에서 설명했듯, 양의 질량 제곱을 가진 물체가 관성운동을 하면서 재는 고유시간은 그 물체가 만든 직선(일반상대론에서 관성운동하는 물체가 그리는 경로는 직선이다)의 길이를 의미한다. 같은 해석을 타키온에 적용하면, 타키온이 관성운동을 하면서 재는 고유시간(tachyonic proper time이라고 부를 수 있을 것이다)은 타키온이 그린 경로의 길이, 혹은 타키온이 지난 경로를 온전히 포함하는 time slice 위에서의 spatial distance에 해당한다.^[각주:1]

이 결론을 임의의 n+1 dS 공간에서 움직이는 타키온들에 적용해보면 재미있는 사실을 몇 가지 알 수 있다. 우선 AdS와 dS의 대칭을 이용하면 임의의 점에서 각기 방향으로^[각주:2] 쏘아보낸 타키온들은 모두 한 점에서 만난다는 사실을 알 수 있다.^[각주:3] FLRW flat 형태의 dS 공간 metric에만 익숙한 분들이라면 약간 놀라울 수 있는 사실. 모든 타키온들이 만나는 점은 타키온을 처음 쏘아보낸 점의 대척점(antipodal point)에 해당한다.

이번에는 좌표를 새로 잡아보도록 하자. 각 방향으로 쏘아보내는 타키온들 중 임의로 하나씩 골라 그 타키온들의 시공간상의 경로가 만들어내는 초평면을 time slice로 하는 좌표계를 만들어보는 것이다.^[각주:4]이렇게 좌표계를 건설하는 것은 dS 공간은 등방적이기 때문에 처음에 쏘아보내는 타키온들의 운동량 분포만 충분히 매끄럽게 만들면 얼마든지 가능하다. 정의상 이 좌표계에서 시간에 해당하는 좌표 t가 상수인 초평면 위를 움직이는 타키온들은 한 점에서 만난다.

결론적으로, 해당 arXiv 글의 결과는 'dS 공간은 모든 spacelike geodesic은 loop를 만든다'는 기하학적인 명제를 다르게 해석한 것이라고 할 수 있다. 타키온이 만드는 경로가 bound되어 있으니 무한한 시간동안 살아남지 못하는 것은 당연한 결과인 셈이다.

페이스북 타임라인에 쌍둥이 역설과 관련이 깊은 질문들이 올라와서 이런저런 생각을 해봤다. 이 글은 대충대충 쓸거라 일반상대론에 대한 지식이 어느 정도 있어야 읽을 수 있다는 것을 미리 알려드리며.

쌍둥이 역설이야 다들 아실테니 설명을 제끼기로 하자. 그렇다면 쌍둥이 역설의 기하적인 의미는 무엇일까? (약간의 비약을 넣어) 기하적으로 접근하면 '평면에서는 두 직선을^[각주:1] 두 번 교차시킬 수 없다'는 것을 의미한다.

두 직선을 두번 교차하게 만드는 방법은 공간을 휘는 것이다. 예컨데 구에서 서로 다른 직선 둘을 그리면 두 점에서 교차하게 된다. 일반상대론에서는 중력이 공간을 휘어주는 역할을 하고, 직선은 중력을 따라 자유낙하하는 물체의 궤적이다. 일반상대론에서 직선의 길이는 자유낙하하는 물체의 고유시간이다.

이제 휘어진 공간에서 두 직선의 길이를 비교해 보자. 가장 간단하게 생각해볼 수 있는 방법은 지구를 이용해 공간을 휜 뒤 A는 지구의 원궤도에, B는 머리 위로 똑바로 던져서 다시 받는 궤도에^[각주:2] 놓되 조건을 잘 맞추어서 같은 시간 같은 점에서 출발한 A와 B가 조금 뒤 같은 점에서 다시 만나도록 하는 것이다. 같은 시공간상의 점에서 출발한 두 직선-A와 B가 만드는 시공간상의 궤적-이 다시 한 점에서 만났을 때, 두 직선의 길이는 과연 같을 것인가? (계산을 해보지는 않았지만) 일반적으로 다르리라고 예상할 수 있다. 쌍둥이 역설일까? 물론 아니다. A가 그린 직선과 B가 그린 직선은 분명히 다르기 때문에^[각주:3] A가 그린 직선의 길이와 B가 그린 직선의 길이가 다른 것이 문제가 될 이유는 없다.

문제를 더 꼬아보자. A가 그린 직선과 B가 그린 직선을 구분할 수 없다면? 그런 종류의 공간으로 더 시터르 공간(de Sitter space: dS)와 반-더 시터르 공간(anti-de Sitter space: AdS)이 있다.^[각주:4] 이 공간들 위에서 두 물체 A와 B가 직선을 그리며 운동할 때 A가 그리는 직선과 B가 그리는 직선은 근본적으로 구분이 불가능하다. 따라서 쌍둥이 역설이 생기지 않으려면 (1) A가 그리는 직선과 B가 그리는 직선은 절대로 만나지 않던가(dS공간이 여기에 해당한다) (2) A가 그리는 직선과 B가 그리는 직선이 만났을 때 두 직선의 거리는 똑같아야 한다(AdS공간이 여기에 해당한다).

재미있는 점은 (2)의 경우 A와 B의 상대속도에 무관하게 같은 고유시간 뒤에 다시 만나게 된다는 부분. 이건 다음과 같이 증명할 수 있다. 우리는 A 위에 앉아있다고 하고, B와 C를 준비한다. 이제 B와 C를 (A에 대해) 같은 속력으로 날리되 방향은 다르게 한다. 그리고 공간은 대칭적이므로 B와 C는 동시에 A에 도착하게 된다. 그런데 B와 C 모두 관성운동을 했으므로, 우리는 B나 C 위에 앉아서 이 과정을 구경해도 된다. C에서 이 과정을 볼 경우 A와 B는 일반적으로 다른 속력을 가지고 관성운동을 하므로, 임의의 상대속력을 갖고 출발한 두 관성운동은 항상 같은 고유시간 뒤에 다시 만나게 된다.^[각주:5]

결론: 일반상대론에서의 쌍둥이 역설으로부터 'AdS 공간에서의 한 점에서 출발하는 모든 timelike geodesic은 다른 한 점으로 수렴하며, 그 고유길이(고유시간)은 모두 같다'는 결론을 내릴 수 있다.

P.S. 고전역학에서는 harmonic oscillator가 정확히 똑같은 현상을 보인다. 우주상수를 넣고 아인슈타인 방정식의 구면대칭적인 해를 찾을 때 나오는 답의 $g_{00}$항이 1(또는 convention에 따라 -1)에서 벗어나는 정도를 Newtonian potential로 해석할 수 있는데, 이 potential 항이 harmonic oscillator의 potential을 갖는다는 것과 연결지어 생각할 수 있다.

양자역학에서 가장 유명한 commutator를 뽑으라면 누구나 하이젠베르크의 불확정성 원리를 꼽을 것이다. 아무래도 제일 먼저 발견된 교환이 불가능한 물리량이니까.

그런데 왜 i가 붙을까? 고민해본 사람? 문제는 의외로 쉽게 풀린다. 두 측정가능한 물리량 A와 B를 가정하자. 따라서 A와 B는 에르미트(Hermitian) 연산자이다. 적당한 양자책을 잘 공부했다면 이를 설명할 필요는 없을 터(간단하게 말하자면 고유값(eigenvalue)이 실수가 나와야 해서). 한번 유도해보자.

측정 가능한 물리량의 commutator는 항상 반에르미트(anti-Hermitian) 연산자여야 한다는 결론을 얻는다. 반에르미트 연산자는 단위허수 i를 곱하거나 나눠서 에르미트 연산자로 만들어줄 수 있으니 이제 그 미스테리한 i가 어디에서 튀어나왔는지 알 수 있다.

이제 조금 더 재미있는 명제를 도출해보자.

아직 이상한 점을 눈치 못챘는가? A에 x를, B에 p를 넣어보자.

?!?!

이 비정합성은 commutator가 identity의 배수이기 때문에 나타난다. 다르게 말한다면, 어떤 한 측정량이 다른 측정량과 만드는 commutator가 identity의 배수로 나온다면 그 측정량의 고유상태(eigenstate)는 그다지 예쁜 성질을 갖지 않으며(예컨데 위치 x의 고유상태나 운동량 p의 고유상태는 L2(Square-integrable)공간에 속하지 않는다), 따라서 주의를 기울여 다루어야 한다고 결론지을 수 있다.

참고로 가장 간단(?)한 양자화 방법은 고전역학에서의 Poisson bracket을 양자역학의 commutator로 해석하는 것이기 때문에(Dirac quantisation 혹은 canonical quantisation) 양자역학의 미래가 골치아프다는 것은 확실해졌다. 양자장론이 괜히 머리 뽀개지는게 아니라니까...

실험 세시간을 날려먹고서야 오실로스코프를 가로 단위를 2.5us로 잡고 single로 측정한 뒤에 가로폭을 확대하여 가로 단위를 500ns로 확대(A)한 후 오실로스코프를 새로운 값을 측정할 수 있도록 준비(B)했을 때와 2.5us에서 single로 측정한 후 오실로스코프를 새로운 값을 측정할 수 있도록 준비(B)한 뒤 가로 단위를 500ns로 확대(A)했을 때 오실로스코프가 측정한 값이 달라진다는 것을 알게 되었다. 붕괴된 멘탈을 재조립하면서 증가한 엔트로피를 배출해야 할 필요가 있으니 신나게 뻘글을 배출해 보자.

얼마 전 개미 다섯 마리의 다리 수를 세는 초등학교 문제가 화제가 된 적이 있었다. 5*6이라고 적은 답안을 오답 처리했기 때문이었는데, 6*5라고 써야 한다는 해설을 들은 사람들은 대체로 멘붕에 빠지거나 어떻게든 내신 등수를 내야겠기에 점수차이를 만드려고 오답처리를 한 것이라며 교사를 욕하는 내용이 대부분이었던 것으로 기억한다. 실제로는 곱셈을 가르칠 때 "무엇의 몇 묶음"의 방식으로 가르치기 때문에 순서가 중요하다고 하지만, 두 숫자의 곱은 순서를 바꾸어도 같다는 것이 상식이라고 말하기조차 민망할 정도로 당연하다고 생각하는 일반적인 사람들에게는 이 오답만큼 황당한 것도 없었으리라.

하지만 물리학(...)의 영역으로 가면 온갖 이상한 것들이 나타나기 시작하는데, 두 숫자의 곱 또한 얼마든지 괴상해질 수 있다. 대표적인 예로 하이젠베르크의 불확정성 원리가 있다. 비전공자가 사용한 100가지 경우 중 제대로 사용한 경우는 한가지가 될까 말까 한 불확정성 원리는 정확히는 '한 계(혹은 물체)에서 뽑아낼 수 있는 정보의 한계'를 말한다.

그렇다면 '정보'란 무엇일까? 섀넌은 정보의 양을 '가능한 모든 경우에서 얼마나 좁은 경우의 수로 좁힐 수 있는가'를 이용해 정의했다고 한다. 예를 들어 사람을 찾을 때 '그 사람은 태어났다'라는 명제는 전혀 정보로서의 가치가 없지만, '그 사람은 90년에 태어났다'라는 명제는 어느 정도 정보로서의 가치를 가지며, '그 사람은 90년 4월에 태어났다'라는 명제는 더 많은 정보로서의 가치를 갖는다는 식이다. 물리학에서도 비슷한 식으로 '한 계의 정보'를 정의할 수 있다. 아리스토텔레스의 자연철학에서는 (참고로 아리스토텔레스의 physics를 '물리학'으로 번역하는 경우가 가끔 있는데 올바른 번역은 '형이하학'이다) 한 물체의 위치만 주어지면 미래에 그 물체가 어떻게 운동할지 모든 것을 알 수 있다고 가정했다. 한 계의 정보로 '위치'면 충분하다는 것이다. 물론 실제로 한 물체의 미래를 알고 싶다면 그보다는 더 많은 정보가 있어야 했다. 갈릴레이는 '운동' 또한 위치만큼 중요하다(물리학에서 중요하게 여기는 값들은 변하지 않는 것-불변량-과 일정하게 유지되는 것-보존량-으로 나눌 수 있는데, 갈릴레이는 운동이 보존량이라는 것을 사고실험으로 증명했다)는 것을 논증했고, 뉴턴은 운동을 '한 계의 정보'에 포함시켰다. 따라서 뉴턴의 유산인 고전역학에 따른다면 '한 계의 정보'는 '위치에 대한 정보'와 '운동에 대한 정보' 두 가지 모두를 의미한다.

그렇다면 오늘 이 시각에도 지구 어딘가에서 오용되고 있을 하이젠베르크의 불확정성 원리로 돌아가 보자. 파울리는 한 편지에서 불확정성 원리를 "'운동을 보는 눈'만 뜨거나 '위치를 보는 눈'만 뜰 수는 있지만 둘 다 뜰 수는 없다니!"라고 표현했는데, 이건 위치에 대한 정보와 물체의 운동에 대한 정보 모두를 얻어낼 수는 없다는 것을 의미한다. 아이러니한 점은 이렇게 한 계에서 필요한 모든 정보를 얻어낼 수는 없더라도 양자역학에 따르면 충분히 완벽하게 그 계의 미래에 대한 모든 것을 알 수 있다는 것이다. 그러므로 불확정성 원리의 '확정'은 "미래는 확정지어져 있다"의 확정이 아니라 "상자에 들은 공의 갯수를 확정지을수 없다"의 확정이다. 하이젠베르크는 "xx의 값은 XX다!"라고 자신있게 말할 수 없다는 것이지, '미래는 모르는 것이다'와 같은 약 파는 소리(..)를 한적은 없다.

그렇다면 앞선 초등학교 수학 문제와 불확정성 원리의 관계는 무엇일까? 불확정성 원리의 수학적인 표현은 순서를 바꾸어 곱한 두 숫자의 차이로 나타난다. q를 위치를 나타내는 수로, p를 운동을 나타내는 수로 쓴다면 'qp-pq=i'가 불확정성 원리의 수학적 표현이다. 보다 쉽게 말한다면, 물리학에서는 q에 p를 곱하는 것과 p에 q를 곱하는 것이 같지 않다는 것이다. 가장 생각하기 쉬운 예시는 수1에서 많은 골치를 썩였을 행렬이 있다. 2X3 행렬에 3X2 행렬을 곱하면 3X2 행렬에 2X3 행렬을 곱한 값과 다를 수 밖에 없다. 이렇게 곱하는 순서가 중요한 숫자들은 불우하게 생을 마감한 수학자 아벨의 이름을 따 비아벨(nonabelian) 수라고 부른다.

한편 물리학자들은 하이젠베르크의 불확정성 원리를 다음과 같이 해석하기도 한다. "A를 먼저 측정한 후 B를 측정하는 것과 B를 먼저 측정한 후 A를 측정하는 것은 다른 결과를 가져온다" 이것은 물리학자들이 이 값들을 일종의 함수로 이해하고, 이 값들의 곱을 고등학교 수학에서부터 다루는 함수의 합성-f(g(x))는 x를 함수 g에 넣어 얻은 값을 다시 함수 f에 넣어 얻는 값을 말한다-으로 이해하기 때문이다. 위의 예시를 그대로 따온다면 pq를 'q를 잰 뒤 p를 잰다'로, qp를 'p를 잰 뒤 q를 잰다'로 이해한다는 것이다. 따라서 물리학자들은 'qp-pq=i'란 식을 'p를 잰 뒤 q를 잰 것과 q를 잰 뒤 p를 잰 것의 차이는 i이다'라고 이해한다.

이는 어떤 일을 수행하는데 순서가 중요하다는 것을 의미한다. 슈퍼맨이 되려면 쫄쫄이 위에 팬티를 입어야지 팬티 위에 쫄쫄이를 입어서는 안 되는 것이다(최근에 본 강철남-Man of Steel-에서는 붉은 삼각팬티가 사라지긴 했지만). 이렇게 어떤 과정을 거쳐서 지금의 상태로 오게 되었는가가 미래에 영향을 미치는 것을 경로의존성이라고 부른다. 물리학에서는 강자성체의 자기이력곡선(말만 어렵지 철이 자석되는 것을 말한다)이 대표적인 예이긴 한데, 너무 물리 이야기만 했으니 조금 다른 이야기를 해보려고 한다. 보다 극명하고 피부에 와 닿는 경로의존성이라면 단연 대통령제를 꼽을 수 있지 않을까. 서구에서는 꽤나 잘 정착된 이 제도는 몇몇 국가에서는 전제군주정의 현대적 변형으로 정착되어 있는데, 제도가 동일한데 결과가 다르다면 그 국가가 거쳐 온 역사가 다르기 때문이라는 설명 외의 적절한 설명은 없어 보인다. 과거가 현재를 만들었고 현재를 너머 미래에까지 영향을 미친다는 것이다. 그러니까 사랑하고 있는 여러분, 애인의 과거가 신경쓰인다면 그 과거가 있었기에 지금 사랑하고 있는 현재의 애인도 있는 것임을 이해하려 노력하시길 바랍니다. 결론이 무언가 이상한 것 같긴 하지만.

통계역학 시험결과가 나왔는데 광자의 화학포텐셜(chemical potential)이 0이라고 가정했다고 점수가 까인 것 때문에 까칠모드로 전환해 써 보는 글. 완벽히 고전적으로 할 경우 어디까지 갈 수 있나 해 봅시다.

1. 먼저 진공이 차 있는 실린더를 가정합니다. 실린더 안은 전자기파로만 채워지고 양자역학적으로 말하면 photon gas에 해당하는 radiation continuum으로 채워진다고 가정하겠습니다. '광자'라는 개념 자체가 없으므로 광자의 수 dN은 등장하지 않습니다.

2. 실린더 안의 radiation continuum을 설명할 때 쓸 변수를 T와 V로 고정하고 이것으로 충분하다고 가정합니다.

3. 여기까지의 가정에서 다음 두 정리를 얻습니다.

3.1. 에너지 U는 extensive variable입니다. 따라서 같은 extensive variable인 V에 대해 선형적으로만 영향을 받을 수 있습니다. 그러므로 U/V=u(T)라는 결론을 얻습니다. 엔트로피 S 또한 extensive variable이기 때문에 부피에 선형적으로 비례하고 S/V=s(T)라는 결론을 얻습니다.

3.2. 압력(있다고 가정할 경우) p는 intensive variable입니다. 따라서 V와는 무관한 변수여야 하며, p=p(T)를 얻습니다.

4. 상태방정식 u=3p를 얻어야 하는데, 이 부분이 제일 까다로와 보이네요. 일단

4.1. 상대론적인 물질은 E/P=c라는 방정식을 만족합니다. 여기서 P는 운동량입니다.

4.2. 임의의 방향으로 분포된 P로부터 압력을 구하면 p = Pc/3V를 얻습니다.

통과한 평균 운동량 = (면적 * 통과한 수직길이 = 통과한 부피) * [(단위부피당 존재하는 운동량의 크기) * 면에 수직한 성분을 위한 코사인] * (고체각 성분) / (반구-한쪽 방향만 생각하므로-의 고체각)

넘어가면서 phi에 대한 부분은 적분으로 날려버립니다.

압력을 구하기 위해 적분하면 p = Pc/3V를 얻네요.

4.3. 에너지를 집어넣습니다. P=E/c=U/c에서 p=U/3V=u/3을 얻습니다.

5. 위의 과정을 통해 U/V=u(T)와 p=u(T)/3을 얻습니다. 독립적인 변수는 T와 V 뿐입니다. 따라서 열역학 제 1법칙을 다음과 같이 정리합니다.

5.1. dT=0으로 두면 s = 4u/3T을 얻습니다.

6. 비열을 구해 봅시다. 정적비열은 다음과 같이 구합니다.

6.1. 정압비열은 구할 수 없습니다. 압력이 온도에 대한 함수로 나오기 때문에 압력을 고정한 채로 온도를 변화시킬 수 없기 때문이죠.

7. 마지막 결과를 조금 꼬아 봅시다. 그러면 고전적으로 스테판-볼츠만 법칙(Stefan-Boltzmann law)을 얻을 수 있습니다.

스테판-볼츠만 상수는 구할 수 없는데, 그 이유는 스테판-볼츠만 상수에는 플랑크 상수가 들어가기 때문이며 플랑크 상수는 양자역학을 도입해야만 등장할 수 있기 때문입니다. 4번까지가 문제가 되고 5번부터는 위키백과에도 나오는 별로 특별할 것은 없는 문제.(신나게 유도해놓고 혹시 있나 해서 찾아봤더니 있었죠...=_=;;)

상대론적인 에너지와 운동량 관계식을 제외하고는 전부 고전열역학적 취급입니다. 양자 가설은 코빼기도 안 비치고, 굳이 태클을 건다면 4.2에서 kinetic theory가 필요하다고 볼 수 있겠네요.

페이스북의 타임라인에 계신 많은 물리 전공자 분들께 질문을 날려보았습니다. 답변을 기다리는 중...

===========================================

음... 제가 뭔가 놓친 것 같은데 제 타임라인의 물리에 목숨 건 여러분들의 도움을 요청합니다....

주제는 '특정 파장의 레이저로 물질의 온도를 몇 도 까지 올릴 수 있는가'. 구글 스칼라로 "laser heating limit"을 검색해봤는데 관련있어 보이는 검색결과는 안 잡히네요(문헌조사가 두뇌 가동 알고리즘에 누락되어 있다는 뼈아픈 지적을 계속 받고 있어서 트레이닝중...).

왜 이런 문제를 생각하게 되었는가는 생략하고(전혀..까지는 아니지만 다른 문제에서 파생된(?) 문제라서요) 단순하게 '레이저의 세기가 물질의 복사에너지와 일치하는 시점에서 온도의 상승이 멈춘다'고 할 경우 다음과 같은 사고실험을 해 볼 수 있지 않느냐는 거죠.

===========================================

아이디어는 다음과 같습니다. 아무리 낮은 온도의 복사체라도 얼마든지 높은 에너지의 광자를 방출할 수 있습니다. 그러면 온도 T를 가진 한 복사체를 포물면거울의 초점에 두고, 반사되어 평면파로 바뀐 복사광을 회절 격자에 쬐어 스펙트럼으로 나눕니다. 그 중 특정 파장에 해당되는 빛만 취하고 나머지는 거울을 이용해 되돌려보냅니다. 유사 레이저를 만드는 거죠. 좀 더 그럴듯하게 하고 싶으면 편광판을 이용하는 방법도 있고요. 어쨌든 이것을 '온도 T의 유사 레이저 발진기'라고 부릅시다.

'온도 T의 유사 레이저 발진기'를 병렬로 연결합니다. 그러면 나오는 유사 레이저의 세기를 얼마든지 올릴 수 있겠죠(쓰다 보니 자신없어진 부분). 그러면 '온도 T의 유사 레이저 발진기'를 수십만개 연결해서 물체A를 가열하기 시작합니다. 물체A의 에너지는 계속 오르다가 어느 시점에서 평형을 이룰 텐데, 만약 이 평형을 이루는 온도가 레이저의 세기에만 의존한다면 충분히 많은 '온도 T의 유사 레이저 발진기'를 병렬로 연결하는 것으로 물체A의 온도를 T 이상으로 끌어올릴 수 있다는 말이 됩니다. 수많은 '온도 T의 유사 레이저 발진기'로 물체A를 T1(T1>T)으로 가열하는 거죠.

여기서 잠깐. 열역학 2 법칙에 따르면 더 낮은 온도에서 더 높은 온도로 열을 전달할 수는 없습니다(GRE Physics 9277인가에 나왔던 문제라 기억하고 있습니다. 틀렸거든요(...)).

...어라?

============================================

일단 보이는 '현실적'인 불가능한 부분은 과연 '완벽한 반사체'가 존재하냐는 것인데요, 빛을 반사하는 과정에서 반사체의 온도가 상승할 가능성을 무시할 수 있느냐는 질문이 되겠네요.

두 번째로 이렇게 유사 레이저를 제작한다고 해도 그 유사 레이저를 병렬로 연결하면 과연 위상이 잘 맞아들어가서 유사 레이저의 광도가 증가할 것인가의 문제가 있습니다. 이 경우엔 레이저의 광도에 해당하는 흑체복사온도가 있다는 결론이 나올테니(유사 레이저의 세기는 흑체복사로 방출되는 복사광의 해당 파장에서의 세기 이상은 못 가질테니까요) 레이저의 광도와 온도를 직접적으로 대응시키는 방법이 생기네요. 문제 해결? 그런데 평균이 0인 정규분포를 따르는 변수를 모으면 모을수록 그 합의 분산은 증가하는데 꼭 광도가 어느 정도 이상의 값은 가지지 못할 것이라고 결론내리는 것이 너무 성급한 것은 아닌가 싶기도 합니다.

나머지 하나는 이 이상한(?) 현상을 받아들이고 다른 해석(?)을 하는 것. 물체A의 에너지를 물체A의 온도의 함수로 보고 canonical ensemble처럼 처리해서(온도 T의 reservior와 반응하는 것으로 생각하는 거죠) 평형상태 온도가 확률이 극대화가 된다는 것을 보이는 것인데(density of state를 고려해야 할 테니 잘 하면 한 계의 엔트로피 계산에도 쓸 수 있겠네요.) 신나는 계산이 기다리고 있죠...=_=;; 어떻게 계산하는가와 원하는 결과가 나올 것인가는 일단 옆으로 치워 두고...

Rev. 07Nov13

흑체복사에서 벗어나는 radiation의 분포 때문에 물질 내부의 상태는 equilibrium distribution이 아닙니다. 해당 파장의 radiation의 흡수율이 급격히 떨어지게 된다는 뜻. 이걸 고려해야 하는데, 이게 말이야 쉽지...=_=;;

더 이상 canonical distribution을 갖지 않는 상태에 대한 연구가 될 듯 합니다.

글을 공개로 바꾸면서 log를 다시 보니 난 수학에서나 요구할 법 한 논리적 엄밀성을 추구하는 별로 좋지 않은 버릇이 있는지도 모르겠다. 과감한 일반화가 물리의 미덕인데...

이전에 쓴 글 중 양자역학의 유래라는 글이 있었다. 현대 양자역학의 근간이 되는 파동방정식 풀이법과 행렬을 이용한 선형대수 연산 및 고유값을 사용하게 된 기원 등을 다룬 글인데,^[각주:1] 오랜만에 덧붙일만한 내용이 생각나서 새로운 글을 쓰기로 했다.

저번 글에서 양자역학이 형성되어 온 두가지 갈래길을 알아보았다. 이번에는 그 두 갈래길이 남아 아직도 영향을 미치고 있는 묘사(picture)에 대해 살펴보자.

수업을 듣던 중 교수님께서 에너지나 운동량 등의 측정값이 양자화되는 이유를 질문하셨다. 누군가가 경계조건(boundary condition)으로 고유값이 결정되기 때문이라고 했고 교수님은 공부를 열심히 했다고 칭찬하시고는 넘어가셨는데 필자가 보기에는 반만 맞는 답이었다. 하지만 타과생인지라 물리학과에 반기를 들기보다는 조용히 넘어갔다. 어째서 반만 맞는 답일까?

양자역학은 두 경로를 통해 발전했다. 하나는 슈뢰딩거(Erwin R. Schrödinger)의 '파동성을 핵심으로 하는 파동역학'이고, 나머지 하나는 하이젠베르크(Werner Heisenberg)의 '양자성을 핵심으로 하는 행렬역학'이다. 파동역학을 양자역학의 원류로 본다면 물리량이 양자화되는 이유는 경계조건이 존재하기 때문인 것이 맞다. 하지만 행렬역학을 양자역학의 원류로 본다면 물리량의 양자화는 공리(postulate)가 된다. 실제 양자역학은 두 원류가 합쳐진 형태로 발전했기 때문에 이런 의미에서 그 답은 반만 맞는 것이다. 그렇다면 이 두가지 관점은 어떻게 남아있을까?

슈뢰딩거의 파동역학은 전자파(electron wave-electromagnetic wave가 아니다!)와 같이 물체에게 파동성이 존재하므로 이미 존재하는 파동광학 등의 결과를 물질로 확장하는 것으로부터 출발하였다. 때문에 시간에 따라 변하는 것은 물질의 상태(state)가 되고, 이것이 반영되어 측정하는 물리량(operator를 말한다)은 시간에 불변하는 것으로 간주되었다. 빛이 화면에 닿아 상을 만들 때 화면의 상태가 변하기 때문에 화면에 그려지는 상이 변화한다고 보기보다는 빛의 상태가 변하기 때문에 상이 변화한다고 생각하는 것이 더 자연스럽지 않은가? 우리가 존재하는 공간이 변화한다고 보는 것보다는 그 공간에 놓인 물질이 변화한다고 보는 것이 아무래도 자연스럽기 때문에 대부분의 학부 양자역학 교재에서는 슈뢰딩거 묘사(Schrödinger picture)를 쓰는 경우가 많다. 슈뢰딩거 묘사를 쓸 경우 운동방정식은 다음과 같다. 잘 보면 고전적인 파동방정식과 닮았다.

$$\dot{\left|\psi\right>}=\frac{\mathbf{H}}{i\hbar}\left|\psi\right>$$

이번엔 하이젠베르크의 행렬역학을 따라가 보자. 하이젠베르크의 행렬역학은 전 글에서 설명했다시피, 물리량을 측정할 경우 그 값이 양자성을 가진다는 것에서부터 출발하였다. 수소원자스펙트럼은 불연속적으로 분포되어있지 않은가. 그렇기 때문에 하이젠베르크에게 변화하는 것은 물질의 상태가 아닌 물질의 측정값, 즉 물리량이 변화하게 된다. 같은 물질을 다른 시간에 측정하면 다른 물리량을 내놓는 것이므로 물질은 그대로 있고 물리량이 변화해야 한다는 의미이다. 안을 알 수 없는 기계장치가 들어있는 상자가 있고 그 상자의 벽에 화면이 설치되어 있어 시시각각 변화하는 숫자를 보여준다고 상상해보자. 이 경우 상자 자체가 변화한다기 보다는 상자의 화면에 찍히는 숫자가 변화한다고 보는 것이 자연스럽다. 하이젠베르크 묘사(Heisenberg picture)를 쓸 경우 운동방정식은 다음과 같다. 해밀토니안 역학에서 이런 방정식을 본 적이 있을 것이다.

$$\dot{\mathbf{A}}=\frac1{i\hbar}\left[\mathbf{A},\mathbf{H}\right]+\frac\partial{\partial{t}}\mathbf{A}$$

마지막으로 흔히 상호작용 묘사(interaction picture) 혹은 폴 아드리엔 모리스 디락(Paul Adrien Maurice Dirac)의 이름을 딴 디락 묘사(Dirac picture)를 생각해보자. 이 묘사방법은 양자장론(Quantum Field Theory)이 등장하면서 입자가 만들어지고 사라지기니 특정한 상태를 규정짓기가 힘들어지자 도입한 것으로 볼 수 있다. 물리적인 계(system)의 진화를 규정짓는 것이 해밀토니안(Hamiltonian)인데 이 묘사에서는 해밀토니안을 두가지로 나눈다. 일반적으로 우리가 측정하는 '입자'를 만들어주는 자유장 해밀토니안(free field Hamiltonian)과^[각주:2] 이 입자들 사이의 상호작용을 기술하는 상호작용 해밀토니안(interaction Hamiltonian)으로 나누고, 각각 H_0와 H_int로 이름붙인다. 우리가 측정하는 모든 물리량은 자유장 해밀토니안에 따라 변화하고, 우리가 측정할 대상이 되는 상태들은 상호작용 해밀토니안에 따라 변화한다. 하이젠베르크 묘사를 설명하면서 쓴 예제를 사용해 본다면 상자의 화면에 등장하는 숫자가 변화하는데, 상자 자체도 조금씩은 모양을 바꾼다는 것으로 생각할 수 있다. 상자의 모양에 따라 화면에 등장하는 숫자 또한 영향을 받는다면 1. 상자의 모양마다 숫자가 어떻게 나타나는지 2. 상자의 모양이 시간에 따라 어떻게 변화하는지로 나누어 설명하는 것이 편리하다. 때문에 상호작용 묘사에서는 운동방정식이 조금 복잡하다.

$$\mathbf{H}=\mathbf{H_0}+\mathbf{H_{int}}\\ \dot{\mathbf{A}}=\frac1{i\hbar}\left[\mathbf{A},\mathbf{H_0}\right]+\frac\partial{\partial{t}}\mathbf{A}\\ \dot{\left|\psi\right>}=\frac{\mathbf{H_I}}{i\hbar}\left|\psi\right>\\\\ \text{where }\mathbf{H_I}\text{ is the solution of}\\ \dot{\mathbf{H_I}}=\frac1{i\hbar}\left[\mathbf{H_I},\mathbf{H_0}\right]+\frac\partial{\partial{t}}\mathbf{H_I}\\ \mathbf{H_I}(t=t_0)=\mathbf{H_{int}}$$

물리 덕후 소리를 들을 정도로 이곳 저곳 다 파고 들어가며 닥치는대로 공부하다 보니 물리학 개념이 어떻게 발전해왔는가에 대해서도 이것 저것 알게 된 것이 많다. 아무래도 이런 이해가 있다 보니까 정리가 좀 잘 되는듯. 다음 학기 학부 졸업논문이나 잘 써야 할텐데...

\gamma(\theta)=2\alpha V_\infty\frac{\cos(\theta)-1}{\sin(\theta)}\\x=\frac{c}2(1-\cos(\theta))

양자역학에서 상태는 추상적인 켓(ket)벡터

$$\left|\psi\right\rangle$$

로 나타난다. 이 벡터가 시간에 따라 진화하는 법칙이 슈뢰딩거(E. Schrödinger) 방정식으로, 1926년 처음으로 변위(x)에 대한 식을 유도해낸 이의 이름을 붙인 것이다. 당시 슈뢰딩거가 식을 유도해내었을 때에는 위 벡터를 변위공간에 투영한 것(

$$\psi(x)\equiv\left\langle{x}\middle|\psi\right\rangle$$

)의 시간에 따른 진화를 다루는 방정식이었고, 그 방정식의 생김새를 보고 파동함수라고 이름붙였다. 나중에 상태를 추상적인 벡터로 나타내기 시작한 것은 디랙(P.A.M. Dirac)의 업적이다.

^[각주:1]

$$i\hbar\frac\partial{\partial{t}}\Psi(x)=-\frac{\hbar^2}{2m}\frac{d^2}{dx^2}\Psi(x)+V(x)\Psi(x)$$

1차원, 입자 하나의 슈뢰딩거 방정식

x가 이상하게 쓰인건 무시하자

$$m_1\ddot{x_1}=k(x_2-x_1-s)\\m_2\ddot{x_2}=-k(x_2-x_1-s)$$

또는,

$$m_1\ddot{y_1}=k(y_2-y_1)\\m_2\ddot{y_2}=-k(y_2-y_1)\\y_1\equiv{x_1},~ y_2\equiv{x_2-s}$$

$$\ddot{(m_1y_1+m_2y_2)}=0 \\\ddot{(y_1-y_2)}=-\frac{k(m_1+m_2)}{m_1m_2}(y_1-y_2)$$

$$\ddot{y_1}=\frac{k}{m_1}(y_2-y_1)\\\ddot{y_2}=-\frac{k}{m_2}(y_2-y_1)$$

$$\ddot{X}=AX \\X=\left( \begin{array}{c}y_1\\y_2\end{array} \right) \\A=\left( \begin{array}{cc} -\frac{k}{m_1} & \frac{k}{m_1} \\ \frac{k}{m_2} & -\frac{k}{m_2} \end{array} \right)$$

$$y=A\cos(\omega{t})+B\sin(\omega{t})$$

$$y=Re[Ae^{i\omega{t}}]$$

$$\ddot{y}=\frac{d^2}{dt^2}Re[Ae^{i\omega{t}}]=Re\left[\frac{d^2}{dt^2}\{Ae^{i\omega{t}}\}\right]=Re[-\omega^2Ae^{i\omega{t}}]$$

$$X=\chi{e^{i\omega{t}}}~,\frac{d}{dt}\chi=0$$

$$\ddot{X}=-\omega^2X=AX\\(A+\omega^2I)X=0$$

2012.11.08
추가할 내용은 새 글로 올리기로 했다. 다음 글도 읽어보시길.

2012/11/08 - 양자역학의 유래(2)