2009. 12. 30. 23:29 Interests/RubiksCube
어느 큐브를 질러야 잘 질렀다고 소문이 날까

'Interests > RubiksCube' 카테고리의 다른 글
| v-cube 7 (0) | 2010.02.19 |
|---|---|
| 가진 큐브들에 대한 간단한 잡담 (1) | 2010.01.04 |
| 444 루빅스 마무리 해법 (12) | 2009.01.28 |
| 아직 죽지 않았다. (0) | 2008.09.13 |
| 기록 갱신 (0) | 2007.12.18 |
2009. 12. 30. 23:29 Interests/RubiksCube

| v-cube 7 (0) | 2010.02.19 |
|---|---|
| 가진 큐브들에 대한 간단한 잡담 (1) | 2010.01.04 |
| 444 루빅스 마무리 해법 (12) | 2009.01.28 |
| 아직 죽지 않았다. (0) | 2008.09.13 |
| 기록 갱신 (0) | 2007.12.18 |
2009. 12. 29. 22:06 Daily lives
| 눈이 왔네요 (0) | 2010.01.04 |
|---|---|
| 새해 두번째 글 (0) | 2010.01.01 |
| 책을 읽다가 (0) | 2009.12.21 |
| 불태웠어... (4) | 2009.12.18 |
| 학부생은 뭘 해도 교수님을 이길 수 없습니다. (0) | 2009.12.10 |
2009. 12. 28. 18:13 Writer
| 무적의 거짓말: 통계 (0) | 2010.01.23 |
|---|---|
| 대한민국이 살아남을 방법? (0) | 2010.01.04 |
| 아바타: 그래픽 말고는 건질 것 없는 영화 (8) | 2009.12.28 |
| 호혜적 인간과 자연선택 (2) | 2009.11.08 |
| 대한민국의 이공계는 호구다 (0) | 2009.11.03 |
2009. 12. 28. 01:21 Writer
 |
아바타 -  제임스 카메론 |
| 대한민국이 살아남을 방법? (0) | 2010.01.04 |
|---|---|
| 자본주의 세상에서 산다는 것 & 줏어먹는 조선일보 (0) | 2009.12.28 |
| 호혜적 인간과 자연선택 (2) | 2009.11.08 |
| 대한민국의 이공계는 호구다 (0) | 2009.11.03 |
| 동서양 천문학의 교류에 대한 소고 (0) | 2009.09.30 |
\left|P(\bold{a},\bold{b})-P(\bold{a},\bold{c})\right|\le1+P(\bold{b},\bold{c})\left|\chi_1\right\rangle=\sqrt{\frac13}\left|\uparrow\right\rangle_e\left|\downarrow\right\rangle_p-\sqrt\frac23\left|\downarrow\right\rangle_e\left|\uparrow\right\rangle_p
\\\left|\chi_2\right\rangle=\sqrt{\frac13}\left|\uparrow\right\rangle_e\left|\uparrow\right\rangle_p-\sqrt\frac23\left|\downarrow\right\rangle_e\left|\uparrow\right\rangle_pP(\bold{a},\bold{b})=\left|\left\langle\chi_a^+\chi_b^+\middle|\chi_1\right\rangle\right|^2+\left|\left\langle\chi_a^-\chi_b^-\middle|\chi_1\right\rangle\right|^2-\left|\left\langle\chi_a^+\chi_b^-\middle|\chi_1\right\rangle\right|^2-\left|\left\langle\chi_a^-\chi_b^+\middle|\chi_1\right\rangle\right|^2P(\bold{a},\bold{b})=\left\langle\chi_1\middle|\bold{\sigma_a}\otimes\bold{\sigma_b}\middle|\chi_1\right\rangle\bold{\sigma_a}=\left|\chi_a^+\middle\rangle\middle\langle\chi_a^+\right|-\left|\chi_a^-\middle\rangle\middle\langle\chi_a^-\right|\\
\bold{\sigma_b}=\left|\chi_b^+\middle\rangle\middle\langle\chi_b^+\right|-\left|\chi_b^-\middle\rangle\middle\langle\chi_b^-\right|| 양자장론 참고자료 (0) | 2013.01.05 |
|---|---|
| 전자기학 교재(?) (0) | 2010.01.28 |
| 우월한 고전역학 (0) | 2009.12.09 |
| Lagrangian in Electromagnetism (4) | 2009.11.07 |
| 가진 물리학/공학 교재들 (7) | 2009.09.30 |
2009. 12. 21. 19:10 Daily lives
 |
자본주의를 의심하는 이들을 위한 경제학 -  조지프 히스 지음, 노시내 옮김/마티 |
| 새해 두번째 글 (0) | 2010.01.01 |
|---|---|
| 학점이 나온다 -_-+ (0) | 2009.12.29 |
| 불태웠어... (4) | 2009.12.18 |
| 학부생은 뭘 해도 교수님을 이길 수 없습니다. (0) | 2009.12.10 |
| 구 안밖 뒤집기 (2) | 2009.12.04 |
2009. 12. 18. 00:51 Daily lives

| 학점이 나온다 -_-+ (0) | 2009.12.29 |
|---|---|
| 책을 읽다가 (0) | 2009.12.21 |
| 학부생은 뭘 해도 교수님을 이길 수 없습니다. (0) | 2009.12.10 |
| 구 안밖 뒤집기 (2) | 2009.12.04 |
| AIDS와 자연선택, 그리고 간단한 통계 (0) | 2009.12.02 |
2009. 12. 17. 01:02 Mathematics
| 루빅스로 배우는 군론 (0) | 2010.01.27 |
|---|---|
| 무한대의 비교: 자연수와 실수 (0) | 2010.01.13 |
| 각종 변환들 (0) | 2009.12.15 |
| Fourier 변환의 고유함수 (0) | 2009.12.15 |
| 적분놀이 (0) | 2009.12.05 |
2009. 12. 15. 19:36 Mathematics


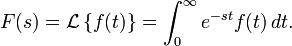
| 무한대의 비교: 자연수와 실수 (0) | 2010.01.13 |
|---|---|
| Laplace 변환을 이용한 미분방정식 풀이 (2) | 2009.12.17 |
| Fourier 변환의 고유함수 (0) | 2009.12.15 |
| 적분놀이 (0) | 2009.12.05 |
| Tensor(1) (2) | 2009.10.16 |
2009. 12. 15. 19:08 Mathematics
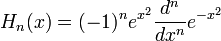
| 무한대의 비교: 자연수와 실수 (0) | 2010.01.13 |
|---|---|
| Laplace 변환을 이용한 미분방정식 풀이 (2) | 2009.12.17 |
| 각종 변환들 (0) | 2009.12.15 |
| 적분놀이 (0) | 2009.12.05 |
| Tensor(1) (2) | 2009.10.16 |
2009. 12. 14. 23:41 Physics/Speculations
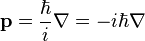
\langle{p}\rangle=\int\psi^{\star}{p}\psi{dx}p_{classical}=m\frac{d}{dt}\langle{x}\rangle=m\frac{d}{dt}\int\psi^\star{x}\psi{dx}m\frac{d}{dt}\int\psi^\star{x}\psi{dx}=\int\psi^\star{\frac{\hbar}{i}\frac{d}{dx}}\psi{dx}\hat{p}=\frac{\hbar}{i}\frac{d}{dx}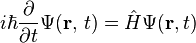
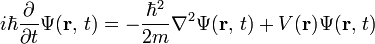
| 양자역학의 유래 (4) | 2010.01.19 |
|---|---|
| 복소수의 필연성 (0) | 2010.01.19 |
| 요즘 하는 생각 (0) | 2009.12.04 |
| Time operator? (2) | 2009.10.20 |
| 왜 하필이면 Hamiltonian 연산자인가? (0) | 2009.10.17 |
2009. 12. 10. 18:27 Daily lives


| 책을 읽다가 (0) | 2009.12.21 |
|---|---|
| 불태웠어... (4) | 2009.12.18 |
| 구 안밖 뒤집기 (2) | 2009.12.04 |
| AIDS와 자연선택, 그리고 간단한 통계 (0) | 2009.12.02 |
| 레알 우로보로스 (0) | 2009.12.01 |
| 전자기학 교재(?) (0) | 2010.01.28 |
|---|---|
| 측정의 평균 (2) | 2009.12.24 |
| Lagrangian in Electromagnetism (4) | 2009.11.07 |
| 가진 물리학/공학 교재들 (7) | 2009.09.30 |
| Operator determination (0) | 2009.04.25 |
2009. 12. 5. 01:04 Mathematics
| 무한대의 비교: 자연수와 실수 (0) | 2010.01.13 |
|---|---|
| Laplace 변환을 이용한 미분방정식 풀이 (2) | 2009.12.17 |
| 각종 변환들 (0) | 2009.12.15 |
| Fourier 변환의 고유함수 (0) | 2009.12.15 |
| Tensor(1) (2) | 2009.10.16 |
2009. 12. 4. 02:48 Physics/Speculations
| 복소수의 필연성 (0) | 2010.01.19 |
|---|---|
| 운동량 연산자에 대해서(1) (7) | 2009.12.14 |
| Time operator? (2) | 2009.10.20 |
| 왜 하필이면 Hamiltonian 연산자인가? (0) | 2009.10.17 |
| 복소수 대칭과 시간대칭 (23) | 2009.04.30 |
2009. 12. 4. 02:32 Daily lives

| 불태웠어... (4) | 2009.12.18 |
|---|---|
| 학부생은 뭘 해도 교수님을 이길 수 없습니다. (0) | 2009.12.10 |
| AIDS와 자연선택, 그리고 간단한 통계 (0) | 2009.12.02 |
| 레알 우로보로스 (0) | 2009.12.01 |
| 얼레...? (0) | 2009.11.07 |
2009. 12. 2. 15:48 Daily lives
| 학부생은 뭘 해도 교수님을 이길 수 없습니다. (0) | 2009.12.10 |
|---|---|
| 구 안밖 뒤집기 (2) | 2009.12.04 |
| 레알 우로보로스 (0) | 2009.12.01 |
| 얼레...? (0) | 2009.11.07 |
| 세상은 넓고.. (0) | 2009.11.02 |
2009. 12. 1. 19:05 Daily lives

| 구 안밖 뒤집기 (2) | 2009.12.04 |
|---|---|
| AIDS와 자연선택, 그리고 간단한 통계 (0) | 2009.12.02 |
| 얼레...? (0) | 2009.11.07 |
| 세상은 넓고.. (0) | 2009.11.02 |
| 아 헌재 진짜 -_- (0) | 2009.10.30 |
2009. 11. 8. 02:12 Writer
| 자본주의 세상에서 산다는 것 & 줏어먹는 조선일보 (0) | 2009.12.28 |
|---|---|
| 아바타: 그래픽 말고는 건질 것 없는 영화 (8) | 2009.12.28 |
| 대한민국의 이공계는 호구다 (0) | 2009.11.03 |
| 동서양 천문학의 교류에 대한 소고 (0) | 2009.09.30 |
| 생명의 존재 방식에 대해서 (0) | 2009.09.27 |
2009. 11. 7. 21:11 Physics
\frac{\partial{L}}{\partial{x_i}}-\frac{d}{dt}\frac{\partial{L}}{\partial{\dot{x_i}}}=0\vec{F}=m\dot{\vec{v}}=q(\vec{E} \vec{v}\times\vec{B})\vec{E}=-\nabla\varphi-\frac{d}{dt}\vec{A}
\\\vec{B}=\nabla\times\vec{A}
\frac{d}{dt}m{\vec{v}}=q(-\nabla\varphi-\frac{\partial}{\partial{t}}\vec{A} \vec{v}\times\nabla\times\vec{A})
\vec{v}\times(\nabla\times\vec{A})=\nabla(\vec{v}\cdot\vec{A})-(\vec{v}\cdot\nabla)\vec{A}\\\frac{d}{dt}m{\vec{v}}=q(-\nabla\varphi-\frac{\partial}{\partial{t}}\vec{A} \nabla(\vec{v}\cdot\vec{A})-(\vec{v}\cdot\nabla)\vec{A})
\frac{\partial}{\partial{t}}\vec{A} (\vec{v}\cdot\nabla)\vec{A})=\frac{d}{dt}\vec{A}\\\frac{d}{dt}m{\vec{v}}=q(-\nabla\varphi \nabla(\vec{v}\cdot\vec{A})-\frac{d}{dt}\vec{A})\\0=\nabla(-q\varphi q\vec{v}\cdot\vec{A})-\frac{d}{dt}(m\vec{v} q\vec{A})
\frac{\partial}{\partial{x_i}}(-q\varphi q\dot{x_j}A_j)-\frac{d}{dt}(m\dot{x_i} qA_i)=0\\\frac{\partial}{\partial{x_i}}(-q\varphi q\dot{x_j}A_j)-\frac{d}{dt}\frac{\partial}{\partial\dot{x_i}}(\frac1{2}m\dot{x_j}^2 q\dot{x_j}A_j)=0
L=\sum_j\frac1{2}m\dot{x_j}^2-q(\varphi-\dot{x_j}A_j)=\frac1{2}m\vec{v}\cdot\vec{v}-q(\varphi-\vec{v}\cdot\vec{A})
| 측정의 평균 (2) | 2009.12.24 |
|---|---|
| 우월한 고전역학 (0) | 2009.12.09 |
| 가진 물리학/공학 교재들 (7) | 2009.09.30 |
| Operator determination (0) | 2009.04.25 |
| Dirac Delta orthonormality (2) | 2009.04.18 |