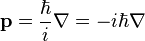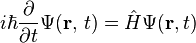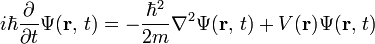'운동량' 태그의 글 목록

'운동량'에 해당되는 글 4건

2009. 12. 15. 19:08 Mathematics

Fourier 변환의 고유함수

수학적 변환에 대해서 글을 쓰다가 재미있는 것을 발견했다. Hermite 다항식이 Fourier 변환의 고유함수라는 것. http://en.wikipedia.org/wiki/Fourier_transform#Eigenfunctions

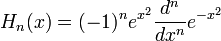
$H_n(x)=(-1)^n e^{x^2}\frac{d^n}{dx^n}e^{-x^2}\,\!$

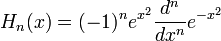
n번째 Hermite 다항식. Wikipedia: Hermite polynomials

Hermite 다항식은 조화진동자 문제에서 등장하는 파동함수라는 것을 생각해보면 재미있다.^[각주:1] 하긴, Hamiltonian은 운동량을 기준으로 쓰든지 위치를 기준으로 쓰든지 생김새 자체는 동일하고, 양자물리에서 Fourier 변환이 basis를 바꾸어주는 변환이라는 것을 생각해보면 이해가 갈 것 같기도 하다. 닮은 방정식의 해는 분명히 닮았을테니 말이다.

$http://www.sitmo.com/gg/latex/latex2png.2.php?z=100&eq=H%3D%5Cfrac%7Bp%5E2%7D%7B2m%7D%2B%5Cfrac%7Bm%5Comega%5E2%7D2x%5E2$

p의 제곱과 x의 제곱으로만 이루어진 Hamiltonian.

$http://www.sitmo.com/gg/latex/latex2png.2.php?z=100&eq=%5Cleft%5Clangle%20x%20%7C%20%5Cpsi_n%20%5Cright%5Crangle%20%3D%20%5Csqrt%7B%5Cfrac%7B1%7D%7B2%5En%5C%2Cn!%7D%7D%20%20%5Cleft(%5Cfrac%7Bm%5Comega%7D%7B%5Cpi%20%5Chbar%7D%5Cright)%5E%7B1%2F4%7D%20%20e%5E%7B%0A-%20%5Cfrac%7Bm%5Comega%20x%5E2%7D%7B2%20%5Chbar%7D%7D%20H_n%5Cleft(%5Csqrt%7B%5Cfrac%7Bm%5Comega%7D%7B%5Chbar%7D%7D%20x%20%5Cright)%2C%20%5Cqquad%20n%20%3D%200%2C1%2C2%2C%5Cldots.$

위 Hamiltonian의 x공간 해. H_n은 n번째 Hermite 다항식

정확히는 여기에 Gaussian 분포를 덧씌워야 하지만. [본문으로]

저작자표시 비영리 변경금지

'Mathematics' 카테고리의 다른 글

무한대의 비교: 자연수와 실수 (0)	2010.01.13
Laplace 변환을 이용한 미분방정식 풀이 (2)	2009.12.17
각종 변환들 (0)	2009.12.15
적분놀이 (0)	2009.12.05
Tensor(1) (2)	2009.10.16

Posted by 덱스터

2009. 12. 14. 23:41 Physics/Speculations

운동량 연산자에 대해서(1)

양자물리를 Griffith 책으로 공부하다 보면 나타나는 의문이 참 많다. 그 중에서 내가 가장 큰 의문을 가졌던 것은 운동량 연산자에 대한 것이었다. 어째서 운동량 연산자는 x로 span된 힐베르트 공간에서 미분으로 나타나는 것일까?

$\mathbf{p}={\hbar\over i}\nabla=-i\hbar\nabla$

3차원 공간에서 운동량 연산자. Wikipedia: Momentum operator

그 이름이 암시하듯이, 운동량이란 물체의 운동 즉 시간과는 떼어놓고 생각할 수 없는 존재이다. 그런데 어째서 운동량을 나타내는 연산자는 시간에 무관한 것일까?

맨 처음 운동량 연산자를 유도해내는 과정을 보고서 내가 느낀 것은, '운동량에 대응하는 정보가 파동함수에 들어 있고, 그 정보는 어떤 연산을 통해서 외부에 나타난다. 따라서, 운동량의 고전적인 정의를 이용해서 운동량에 해당하는 연산자를 유도해내는 것은 아닐까?'였다.

1. 어떤 연산이 있어 운동량에 대응된다.
\langle{p}\rangle=\int\psi^{\star}{p}\psi{dx}

2. 고전적인 운동량에 해당하는 값은 다음과 같다.
p_{classical}=m\frac{d}{dt}\langle{x}\rangle=m\frac{d}{dt}\int\psi^\star{x}\psi{dx}

3. 이미 알려진 Schrodinger 방정식을 적절히 손보면, 다음 식을 얻는다.^[각주:1]m\frac{d}{dt}\int\psi^\star{x}\psi{dx}=\int\psi^\star{\frac{\hbar}{i}\frac{d}{dx}}\psi{dx}

4. 여기서 운동량에 해당하는 연산을 찾을 수 있다.(연산자를 강조하기 위해 ^ 사용)
\hat{p}=\frac{\hbar}{i}\frac{d}{dx}

하지만 문제는, 우리가 알고 있는 Schrodinger 방정식 자체가 운동량 연산자를 가정하는 것에서 출발했다는 것이다. 보통 Schrodinger 방정식은 다음과 같은 형태로 쓴다.

$i\hbar\frac{\partial}{\partial t} \Psi(\mathbf{r},\,t) = \hat H \Psi(\mathbf{r},t)$

하나의 계에 대한 Schrodinger 방정식

$i\hbar\frac{\partial}{\partial t} \Psi(\mathbf{r},\,t) = -\frac{\hbar^2}{2m}\nabla^2\Psi(\mathbf{r},\,t) + V(\mathbf{r})\Psi(\mathbf{r},\,t)$

입자 하나에 대한 Schrodinger 방정식. Wikipedia: Schrodinger equation

H는 Hamiltonian 연산자로, 고전역학에서 사용하는 Hamiltonian이라는 물리량에 해당한다. 일반적인 경우, Hamiltonian은 계 전체의 에너지와 같은 값을 갖는다. 따라서, Schrodinger 방정식은 계를 나타내는 상태함수가 에너지에 비례하여 시간적으로 변화한다는 것을 나타낸다고 볼 수 있다. 그리고 고전적으로 운동에너지는 운동량의 제곱을 질량의 두배로 나눈 값이다. Schrodinger 방정식의 첫 항(Laplacian이 들어가 있는 항)을 잘 보면 바로 앞서 구한 운동량의 제곱을 질량의 두배로 나눈 값, 즉 고전적인 운동에너지라는 것을 알 수 있다. 결국, 우리는 원점으로 돌아온 것이다.^[각주:2] 그렇다면 어떻게 해야 운동량에 해당하는 연산자를 구할 수 있을까?

쓰기 귀찮아서 여기까지만...(여기까지 써놓고 끝날 가능성도 농후)
관심이 가시는 분은 여기를 참조:
http://en.wikipedia.org/wiki/Schr%C3%B6dinger_equation#Derivation
Erwin Schrodinger의 원본을 보고 싶으신 분을 위하여:
http://home.tiscali.nl/physis/HistoricPaper/Schroedinger/Schroedinger1926c.pdf

Griffith 책에 있으니 생략. [본문으로]
Schrodinger 방정식이라는 대전제 안에 운동량에 대한 가정이 포함되어 있고, 우리는 이 보이지 않는 가정을 일련의 과정을 통하여 벗겨낸 것일 뿐이다. [본문으로]

저작자표시 비영리 변경금지

'Physics > Speculations' 카테고리의 다른 글

양자역학의 유래 (4)	2010.01.19
복소수의 필연성 (0)	2010.01.19
요즘 하는 생각 (0)	2009.12.04
Time operator? (2)	2009.10.20
왜 하필이면 Hamiltonian 연산자인가? (0)	2009.10.17

Posted by 덱스터

2009. 10. 17. 01:00 Physics/Speculations

왜 하필이면 Hamiltonian 연산자인가?

Shankar 책을 산지 좀 되었습니다.

심심해서(하라는 시험공부는 안하고) 이전에 Liboff 책에서 재미있게 보았던 대칭성과 보존에 관한 부분을 보았습니다. 보다 보니 이런 부분이 나오더군요.

[...]

We define translational invariance by the requirement

$T^\dag(\epsilon)HT(\epsilon)=H$

[...]

Principles of Quantum Mechanics 2nd Ed., R. Shankar, Springer, 1994, p. 285

저기서 T(epsilon) 연산자는 입실론만큼 전체를 +x 방향으로 옮기는 연산자입니다. 그건 그렇다 치고, 왜 불변성을 Hamiltonian 연산자를 이용해 정의하는 것인지 좀 생각해 보아야겠더군요.

현재는 그저 '기본법칙이 Schrödinger 방정식이기 때문'이라고 결론내렸습니다. 저 항등식을 만족시킨다면 상태함수에 T 연산자를 마음껏 들이대어도 기본법칙에 어긋나지 않거든요.

$\langle\phi_\epsilon\mid{H}\mid\psi_\epsilon\rangle=\langle{T(\epsilon)}\phi\mid{H}\mid{T(\epsilon)}\psi\rangle\\=\langle\phi\mid{T^\dag(\epsilon)HT(\epsilon)}\mid\psi\rangle=\langle\phi\mid{H}\mid\psi\rangle$

왜 왼쪽에 다른 임의의 상태를 들이대냐면, 측정은 저렇게 이루어지기 때문입니다. 양자물리에서 모든 측정량은 저렇게 bra를 붙여서 얻어야 하니 말이지요. (그런데 써놓고 보니 아직도 논리에 구멍이 있는 것 같네요. 좀 더 엄밀하게 해보는 것은 나중에...)^[각주:1]

어찌되었든, T 연산자로 모든 상태를 이동시켜 놓았을 때 임의의 연산자 A는 어떻게 변해야 하는가 생각해 보았습니다. 생각해보니 쉽더군요.

$\langle\phi_\epsilon\mid{A_\epsilon}\mid\psi_\epsilon\rangle=\langle\phi\mid{T^\dag(\epsilon)A_\epsilon}{T(\epsilon)}\mid\psi\rangle=\langle\phi\mid{A}\mid\psi\rangle$

이니까

$A_\epsilon=T^\dag(\epsilon)^{-1}AT(\epsilon)^{-1}$

하지만 T 연산자의 역함수(역연산자?)는 T 연산자의 hermitian conjugate 입니다. 왜 그런지는 A 대신에 I(Identity - 1이라고 생각하시면 됩니다)를 넣어보면 됩니다. I 연산자가 좌표와는 상관있을 리가 없겠죠. 그러면 결국

$A_\epsilon=T^\dag(\epsilon)^{-1}AT(\epsilon)^{-1}=T(\epsilon)AT^\dag(\epsilon)$

이 됩니다. 어째 어디선가 본 행렬형식의 2계텐서 변환방식이 떠오르는군요.

그나저나 시간대칭은 역시 허수의 성질을 이용하는군요. i나 -i나 구분할 수 없다는 그 성질 말입니다. 이건 예전에 적어둔 것이니 링크만 간단히...

2009/04/30 - 복소수 대칭과 시간대칭

ps. 뭐 아실 분들은 아시겠지만 사실 저 T 연산자는 P 연산자, 즉 운동량과 관련이 있습니다. 그래서 운동량 보존이 균일성(위치에 대해 변하지 않음-translational symmetry/invariance)과 동치인 것이구요. 정확히는

$T(\epsilon)=exp{-\frac{{iP}}{\hbar}\epsilon}$

입니다. Taylor 전개를 해 보면 알 수 있는데 그것까지 하기는 귀찮네요. Griffith 책의 연습문제로도 나오니 제가 할 필요는 없겠지요.

이렇게 엄밀한 거 좋아하다가 서너줄이면 끝날 숙제 문제를 한두페이지가량 써제끼는 일이 한두번이 아니네요 -_-;; [본문으로]

저작자표시 비영리 변경금지

'Physics > Speculations' 카테고리의 다른 글

요즘 하는 생각 (0)	2009.12.04
Time operator? (2)	2009.10.20
복소수 대칭과 시간대칭 (23)	2009.04.30
어는점내림/끓는점오름을 다른 상수에서 구하기 (4)	2009.04.24
파동함수... (6)	2009.03.04

Posted by 덱스터

2009. 4. 18. 13:11 Physics

Dirac Delta orthonormality

모멘텀 변환 파동함수는 다음과 같이 나타난다(hbar 표현식을 못 찾아서 저렇게 썼음 -_-;;).

$\!\varphi_p(x)=Ae^{\frac{2\pi ipx}h}$

이 식은 k에 대해서도 쓸 수 있다. 이때 khbar는 p가 된다.

$\!\varphi_k(x)=Ae^{ikx}$

적분구간을 무한대로 해 놓고 두 모멘텀 파동함수(변수는 k)를 적분하면 Dirac Delta fuction이 얻어진다.

$\!\int_{-\infty} ^\infty \varphi_k (x)^\ast \varphi_{k'} (x) dx = 2\pi A^2 \delta (k-k')$

여기서 2pi는 다음과 같은 이유에서 얻어진다. 먼저 적분구간을 [0, 2pi]로 해 보자. 그러면 다음과 같은 관계식이 얻어진다.

$\!\int_{0} ^{2\pi} \varphi_k (x)^\ast \varphi_{k'} (x) dx = 2\pi A^2 \delta _{kk'}$

여기서의 델타는 Kronecker Delta이다. 이제 이 구분된 적분구간을 무한히 확장한다. 그러면 처음에 얻은 식이 얻어진다.(Dirac Delta가 Kronecker Delta의 무한합으로 보는 관점) 이런 연유에서 규격화된 k에 대한 파동함수는 다음과 같이 쓴다.

$\!\varphi_k (x) = \frac {1}{\sqrt{2\pi}} e^{ikx}$

보통의 경우, 일반적인 식은 다음과 같이 쓸 수 있다.

$\!\Phi (k) = \int_{-\infty} ^\infty \varphi_k ^\ast (x) \Psi (x)dx$

$\!\Psi (x) = \int_{-\infty} ^\infty \varphi_x ^\ast (k) \Phi (k)dk$

여기서

$\!\varphi_x (k) = \varphi_k ^\ast (x)$

로 정의한다.

덧. 궁금해하던 건데 마침 친구가 알려주더군요. 책 없이 휘갈기는거라 몇몇 상수는 빠졌을 수도 있습니다.(예를 들어 부호가 바뀌었다던지...)

그나저나 그녀석은 요즘 군론 공부한다던데 -_-;;;; (돌은 학부생이죠 예...-_-;;;;)

덧2. 알고보니 변수가 바뀌었군요 OTL 전부 수정했습니다. 마지막 부분은 외우기 쉽게 하려고 도입한 꼼수입니다 ^^ 책에는 없을거예요(Griffith에 없으니 다른 책에도 아마 없으리라 생각)

저작자표시 비영리 변경금지

'Physics' 카테고리의 다른 글

측정의 평균 (2)	2009.12.24
우월한 고전역학 (0)	2009.12.09
Lagrangian in Electromagnetism (4)	2009.11.07
가진 물리학/공학 교재들 (7)	2009.09.30
Operator determination (0)	2009.04.25

Posted by 덱스터

Dexter's story

'운동량'에 해당되는 글 4건

Fourier 변환의 고유함수

'Mathematics' 카테고리의 다른 글

운동량 연산자에 대해서(1)

'Physics > Speculations' 카테고리의 다른 글

왜 하필이면 Hamiltonian 연산자인가?

'Physics > Speculations' 카테고리의 다른 글

Dirac Delta orthonormality

'Physics' 카테고리의 다른 글

카테고리

태그목록

공지사항

달력

최근에 올라온 글

최근에 달린 댓글

글 보관함

티스토리툴바

« | » 2024.4
일	월	화	수	목	금	토
	1	2	3	4	5	6
7	8	9	10	11	12	13
14	15	16	17	18	19	20
21	22	23	24	25	26	27
28	29	30