2009. 12. 15. 19:36 Mathematics
각종 변환들
좌표변환과 같이 물리적인 의미가 있는 변환 말고 수학적인 변환 위주로 정리.
1. Legendre 변환
고전역학에서는 Hamiltonian에 쓰인다. 열역학에서도 Enthalpy나 Gibbs 자유에너지, Helmholtz 에너지 등에서 나타난다. 미분방정식에서 변수를 바꾸는 데 이용한다.

여기서 라고 정의해주면
라고 정의해주면

이처럼 변수가 바뀌게 된다.
2. Fourier 변환
파동역학 쪽에서 주로 쓰는듯. 양자역학에서는 basis를 위치에서 운동량으로(또는 역으로) 바꿀 때 이용한다. FFT(Fast Fourier Transform)이라고 해서 소리 정보를 디지털 정보로 변환해 저장하는 데 응용하기도 하는 것 같다. 진동 쪽에서도 공명주파수를 구하기 위해 쓰이는 것 같으나 자세한 것은 불명.
기본적으로는 Fourier series에서 주기를 무한대로 확장한 것이다. 때문에 전체구간에서 적분한 값이 존재하지 않으면 쓸 수 없다. 변수는 실수.


위는 일반적인 n차원에서 Fourier 변환을 나타낸다.1 위의 것은 Fourier 변환, 아래 것은 역 Fourier 변환이라고 불린다. 변환시킨 것을 다시 되돌려 놓는다는 의미. 기타 다른 방법으로 쓸 수도 있지만, 이 방법이 대칭성이 보기 좋아 주로 쓰이는 것 같다.
미분방정식을 푸는데 쓸 수 있다. 역변환이 더럽긴 하지만. 여기를 참조.

위의 관계식을 이용해서(부분적분으로 증명할 수 있느나 생략) 미분방정식을 단순한 대수방정식으로 바꾸는 것이다. 경우에 따라서는 convolution도 이용해야 하는 것 같지만...
예시:

3. Laplace 변환
신호쪽에서 쓴다고는 하지만, 사실 어디서 쓰는지 잘 모른다(...). 듣기로는 Fourier 변환의 확장이라고... 특징이라면 Fourier 변환이 함수가 무한대에서 발산하지 않을 것을 요구하지만 여기서는 그런거 없다는 것 정도? 대신 적분구간이 음의 무한이 아니라 0부터 무한이다.(일반적인 경우는 그렇지만, 전체 구간으로 확장하는 경우도 있는듯 하다.)
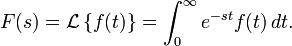
s는 복소수라고 한다.(그런데 난 그렇게 배운 기억이 없다. 뭐지?)2
마찬가지로 미분방정식을 푸는데 쓸 수 있다. 역시 여기 참조. 따로 역변환이 있다고 배운 기억이 없기 때문에 얻어진 변환의 함수꼴을 보고 원래 함수를 추정한다.(적어도 Kreyzig 책에서는 그렇게 푼다.)3

예시는 귀찮으니까 여기로...
최근 글인 2009/12/17 - Laplace 변환을 이용한 미분방정식 풀이참조.
4. Gauge 변환
전자기에서 등장. 듣기로는 핵력에서도 쓰인다는데, 배우지 못한 관계로 생략. 일종의 '기준점을 선택할 자유도'이다. 자세히 적는건 나중에... 그동안은 여기서..
시간나는 대로 추가할 생각이다.
1. Legendre 변환
고전역학에서는 Hamiltonian에 쓰인다. 열역학에서도 Enthalpy나 Gibbs 자유에너지, Helmholtz 에너지 등에서 나타난다. 미분방정식에서 변수를 바꾸는 데 이용한다.
여기서
이처럼 변수가 바뀌게 된다.
2. Fourier 변환
파동역학 쪽에서 주로 쓰는듯. 양자역학에서는 basis를 위치에서 운동량으로(또는 역으로) 바꿀 때 이용한다. FFT(Fast Fourier Transform)이라고 해서 소리 정보를 디지털 정보로 변환해 저장하는 데 응용하기도 하는 것 같다. 진동 쪽에서도 공명주파수를 구하기 위해 쓰이는 것 같으나 자세한 것은 불명.
기본적으로는 Fourier series에서 주기를 무한대로 확장한 것이다. 때문에 전체구간에서 적분한 값이 존재하지 않으면 쓸 수 없다. 변수는 실수.


Wikipedia: Fourier transform
위는 일반적인 n차원에서 Fourier 변환을 나타낸다.1 위의 것은 Fourier 변환, 아래 것은 역 Fourier 변환이라고 불린다. 변환시킨 것을 다시 되돌려 놓는다는 의미. 기타 다른 방법으로 쓸 수도 있지만, 이 방법이 대칭성이 보기 좋아 주로 쓰이는 것 같다.
미분방정식을 푸는데 쓸 수 있다. 역변환이 더럽긴 하지만. 여기를 참조.
위의 관계식을 이용해서(부분적분으로 증명할 수 있느나 생략) 미분방정식을 단순한 대수방정식으로 바꾸는 것이다. 경우에 따라서는 convolution도 이용해야 하는 것 같지만...
예시:
3. Laplace 변환
신호쪽에서 쓴다고는 하지만, 사실 어디서 쓰는지 잘 모른다(...). 듣기로는 Fourier 변환의 확장이라고... 특징이라면 Fourier 변환이 함수가 무한대에서 발산하지 않을 것을 요구하지만 여기서는 그런거 없다는 것 정도? 대신 적분구간이 음의 무한이 아니라 0부터 무한이다.(일반적인 경우는 그렇지만, 전체 구간으로 확장하는 경우도 있는듯 하다.)
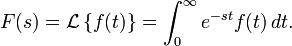
Wikipedia: Laplace transform
s는 복소수라고 한다.(그런데 난 그렇게 배운 기억이 없다. 뭐지?)2
마찬가지로 미분방정식을 푸는데 쓸 수 있다. 역시 여기 참조. 따로 역변환이 있다고 배운 기억이 없기 때문에 얻어진 변환의 함수꼴을 보고 원래 함수를 추정한다.(적어도 Kreyzig 책에서는 그렇게 푼다.)3
예시는 귀찮으니까 여기로...
최근 글인 2009/12/17 - Laplace 변환을 이용한 미분방정식 풀이참조.
4. Gauge 변환
전자기에서 등장. 듣기로는 핵력에서도 쓰인다는데, 배우지 못한 관계로 생략. 일종의 '기준점을 선택할 자유도'이다. 자세히 적는건 나중에... 그동안은 여기서..
시간나는 대로 추가할 생각이다.
'Mathematics' 카테고리의 다른 글
| 무한대의 비교: 자연수와 실수 (0) | 2010.01.13 |
|---|---|
| Laplace 변환을 이용한 미분방정식 풀이 (2) | 2009.12.17 |
| Fourier 변환의 고유함수 (0) | 2009.12.15 |
| 적분놀이 (0) | 2009.12.05 |
| Tensor(1) (2) | 2009.10.16 |


