2010. 5. 1. 23:13 Mathematics
Involute 곡선
수학의 아름다움이라는 글에서 말했듯이 뉴턴 이전의 물리라는 이름을 붙일만한 학문(?)들은 정량적인 분석보다는 정성적인 분석이 주를 이루었다. 중학교 과학 교과과정에 나오는 4원소설과 같은 것들 말이다. 따라서 전통적인(?) 자연과학은 숫자를 자주 사용하는 현대보다는 기하학과 같이 보다 추상적인 학문이었다고 할 수 있다.1 오늘은 그래서 기하학 이야기를 조금 해 보자.
전에 낸 퀴즈의 답은 involute 곡선이다. 정확히는 원의 involute 곡선이 된다. 만드는 방법은 다음과 같다. 먼저 원에 실을 팽팽하게 감아둔다. 그 다음 실의 끝에 펜을 연결하고 실을 팽팽하게 당긴 상태로 실을 푼다. 그러면 펜이 그리는 곡선이 involute 곡선이 된다.
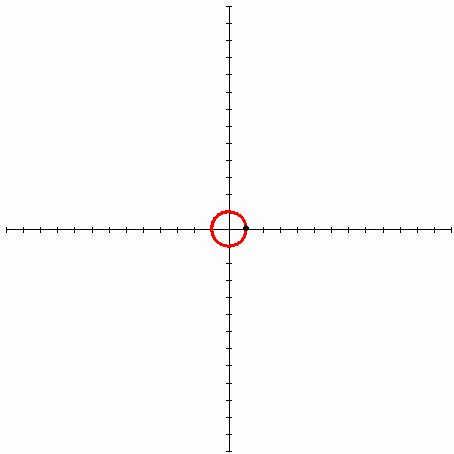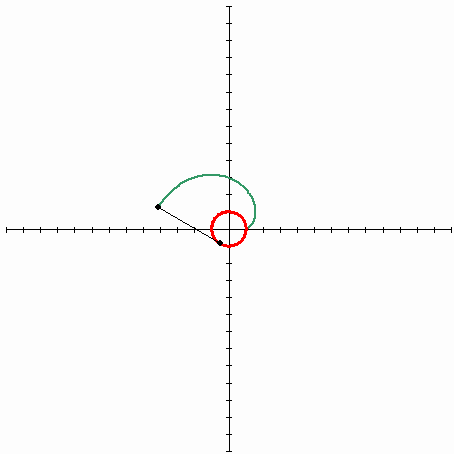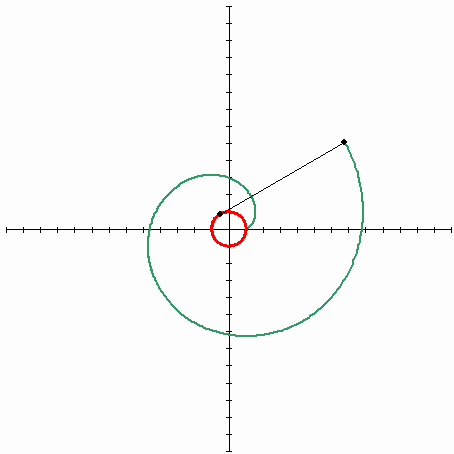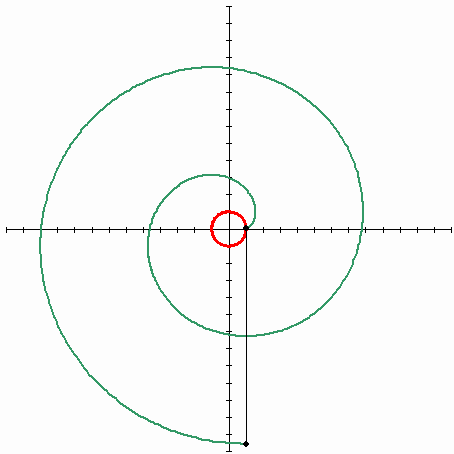
팽팽하게 잡아당겨진 실의 끝은 실과는 항상 수직하게 움직일 수 밖에 없다. 원에 감긴 실을 잡아당긴 채로 풀게 되면 풀려진 실은 원의 접선의 일부가 되고, 따라서 이렇게 그리는 곡선은 원의 어떤 접선을 잡아도 접점에서는 항상 수직하다.
왜 이 곡선이 중요한가는 이 곡선이 원의 어떤 접선을 가져와도 항상 수직하다는 특징 때문이다. 이론적으로 어떤 접촉면에서 마찰을 제외한 모든 힘은 면에 수직하게만 주어진다. 따라서 원의 접선 방향을 따라 힘을 전달하고 싶다면, 원 위에 이 곡선을 기반으로 한 곡면을 만들어 밀어주면 되는 것이다. 기어에 이 곡선이 주로 사용되는 이유이다.2
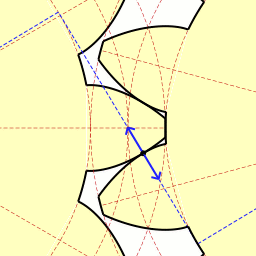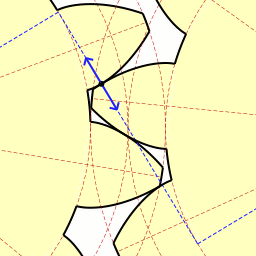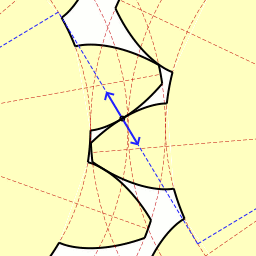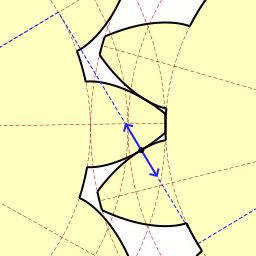
잘 보면 힘이 전달되고 있는 파란선과 두 기어가 접촉하는 면이 항상 수직한 것을 볼 수 있다.
수학은 그리 멀리 떨어진 곳에 있는게 아니다. 단지 눈이 좋지 못해 못 찾아내고 있을 뿐이다.
전에 낸 퀴즈의 답은 involute 곡선이다. 정확히는 원의 involute 곡선이 된다. 만드는 방법은 다음과 같다. 먼저 원에 실을 팽팽하게 감아둔다. 그 다음 실의 끝에 펜을 연결하고 실을 팽팽하게 당긴 상태로 실을 푼다. 그러면 펜이 그리는 곡선이 involute 곡선이 된다.

팽팽하게 잡아당겨진 실의 끝은 실과는 항상 수직하게 움직일 수 밖에 없다. 원에 감긴 실을 잡아당긴 채로 풀게 되면 풀려진 실은 원의 접선의 일부가 되고, 따라서 이렇게 그리는 곡선은 원의 어떤 접선을 잡아도 접점에서는 항상 수직하다.
왜 이 곡선이 중요한가는 이 곡선이 원의 어떤 접선을 가져와도 항상 수직하다는 특징 때문이다. 이론적으로 어떤 접촉면에서 마찰을 제외한 모든 힘은 면에 수직하게만 주어진다. 따라서 원의 접선 방향을 따라 힘을 전달하고 싶다면, 원 위에 이 곡선을 기반으로 한 곡면을 만들어 밀어주면 되는 것이다. 기어에 이 곡선이 주로 사용되는 이유이다.2

잘 보면 힘이 전달되고 있는 파란선과 두 기어가 접촉하는 면이 항상 수직한 것을 볼 수 있다.
수학은 그리 멀리 떨어진 곳에 있는게 아니다. 단지 눈이 좋지 못해 못 찾아내고 있을 뿐이다.
'Mathematics' 카테고리의 다른 글
| Lagrange Multipliers - 라그랑주 승수법 (7) | 2011.01.16 |
|---|---|
| 경계조건의 중요성 - Boundary condition (2) | 2010.08.21 |
| 수학의 아름다움 (2) | 2010.04.24 |
| Power set, again (0) | 2010.04.17 |
| 무한대와 무한대가 만났을 때 (4) | 2010.04.13 |


