2010. 10. 23. 13:00 Physics/Special

철새들이 V자로 비행하는 이유

일단 이 내용은 09년 봄학기 항공역학 기말고사 시험문제였죠. 기초적인 읽을거리 들어갑니다.


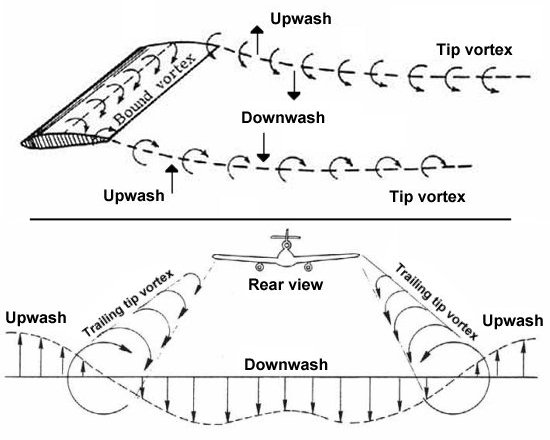
한줄로 요약하면 앞에서 나는 새가 상승기류를 만들고, 그 상승기류를 탄 뒤쪽의 새는 편하게 날아간다는 겁니다. 그러면 그 상승기류는 어디서 나오는 것일까요? 다음 비행기 사진을 살펴 보겠습니다.


Wingtip vortex라 부르는 비행기 날개 끝의 소용돌이입니다. 전투기가 나오는 영화나 애니메이션이라면 항상 등장하는 단골 손님이기도 하구요. 이 소용돌이를 잘 보면 날개 아래 쪽에서 시작해서 밖을 선회하며 날개 위 쪽으로 돈다는 것을 알 수 있습니다. 이 소용돌이가 바로 상승기류의 원인이 되는 것이지요.

Regions of upwash and downwash created by trailing vortices

그렇다면 이 소용돌이가 왜 생기는지 알아야 상승기류에 대해 더 잘 이해할 수 있겠지요. 이 소용돌이는 날기 위해 생기는 어쩔 수 없는 현상입니다. 먼저 비행기가 나는 원리를 생각해 보도록 하겠습니다. 비행기가 나는 원리는 간단합니다. 날개 위 아래로 압력차이를 발생시켜서 날개에 뜨는 힘을 유도하는 것이죠. 압력밥솥 위에 달린 종처럼 생긴 물건이 밥을 할 때 치카치카 거리면서 흔들거리는 이유와도 동일합니다.


이를 위해 비행기 날개의 단면은 위쪽으로 살짝 둥근 형태를 취하게 됩니다. 둥근 모습을 하게 되면 위쪽에 더 빠르게 공기가 흐르게 되는데, 이건 날개가 공기를 위쪽으로 더 많이 밀어내어 그 공기가 뒤로 빠져나가기 위해서는 더 빨리 흘러야 하기 때문입니다. 물이 흘러 나오는 호스의 끝을 쥐어 짜면 물이 엄청나게 세게 튀어나오는데, 그 원리와 비슷합니다.

Watering Plants Fallujah.jpg

그리고 베르누이의 법칙(Bernoulli's Principle)에 따르면 유체는 속도가 빠를수록 낮은 압력을 갖습니다. 같은 밀도라고 하더라도 한 방향으로 흐르면 상대적으로 그 유체의 분자 하나하나가 압력을 전달하는 면에 작용하는 운동량이 적어지기 때문이라고 생각하면 됩니다. 그래서 윗면에는 빠른 공기와 낮은 압력이 분포하게 되고, 아랫면에는 느린 공기와 높은 압력이 분포하게 됩니다. 압력 차가 생겨났기 때문에 비행기는 뜨게 되는 것이지요. 그리고 그 압력 차이 때문에 앞서 나온 소용돌이 또한 발생하게 됩니다.


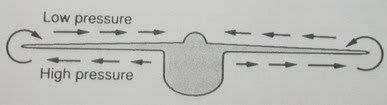
공기는 높은 압력에서 낮은 압력의 방향으로 흐릅니다. 위 그림을 보시면 비행기의 아래쪽에는 높은 압력이, 위쪽에는 낮은 압력이 형성되었다는 것을 보실 수 있습니다. 공기는 그 압력 분포를 따라 이동하는 것이지요. 그리고 그 이동이 날개 끝에서는 소용돌이가 되어 나타나는 것입니다. 바로 이 소용돌이가 선두를 날아가는 새에게서 상승기류를 얻는 원천이 되는 것이지요.

하지만 그렇다고 해서 선두의 새는 손해만 보는 것은 아닙니다. 선두의 양 옆을 날아가는 새들은 선두를 나는 새에게 날개가 더 커지는 효과를 부여합니다. 선두의 새가 느끼는 소용돌이가 감소하게 되는 것이지요. 소용돌이는 진공을 가져오고 진공은 비행시 저항으로 작용하기 때문에 V자 대열은 선두의 새에게도 이득이 되는 셈입니다.

이것으로 글을 마치도록 하겠습니다. 마무리는 역시 멋진 비행기 사진으로... 태양을 날다!!

저작자표시 비영리 변경금지

'Physics > Special' 카테고리의 다른 글

그 많던 종이비행기는 어떻게 다 날았을까  (8) 2013.10.06
자기 단극자의 vector potential  (0) 2011.10.03
[물벽깨-2] 동시성의 상대성이란 무엇인가 - 실체진실의 장 1에대한 반론  (16) 2009.01.08
[물벽깨-1] 특수상대론은 무엇인가  (10) 2008.12.01
특별기획 - 물리의 벽을 깨라!  (6) 2008.11.20
Posted by 덱스터

2010. 5. 30. 13:00 Physics/Speculations

Kutta-Joukowski Theorem, alternate proof(without residue theorem)

항공역학(사실상 유체역학이다만)을 배우다 보니 꽤 간단하면서도 중요한 식들을 보게 되는데, 그중 단연 으뜸이라고 할 수 있는 녀석은 이 녀석이다. Kutta-Joukowski Theorem

L'=\rho_{\infty}V_{\infty}\Gamma

대문자 감마(Gamma)는 circulation이라고 불리는 녀석인데, 여기서는 이렇게 정의한다.

\Gamma=-\oint\vec V\cdot d\vec s

2차원 유동을 다룰 때 나오는 식이다. 예상하겠지만, circulation은 어떤 폐곡선을 따라 적분하느냐에 따라 값이 휙휙 뒤바뀐다. 그리고 전자기학 공부 조금이라도 깊게 한 사람은 알겠지만, Stokes정리에[각주:1] 의해 대문자 감마를 다른 방식으로 구할 수 있다.

\Gamma=-\oint\vec V\cdot d\vec s~~~~~\\=-\int \vec\nabla\times\vec V dA[각주:2]

유체역학에서는 유동장 속도 벡터에 curl을 취한 벡터를 vorticity라고 부른다. 일반적으로 여기에 문자 하나를 배정해 주는데 크시(Xi)를 주로 쓰는 듯. 별로 중요하지는 않아 보이지만. 이 값은 그 위치에서 유동 성분이 어떤 각속도를 가지고 도는지를 나타낸다. 크시의 크기는 각속도의 두배.

\vec\xi=\vec\nabla\times\vec V

항공역학이다 보니 항공기에서 나타나는 유동을 주로 다루게 되는데, 일반적으로 vorticity는 0이다.(이러면 속도 벡터를 모함수의 물매(gradient)로 생각할 수 있어 potential flow라고 부른다.) 단순하게 생각해서 항공기가 앞으로 날아가면 항공기 입장에서는 공기가 앞에서 불어오는 것처럼 보인다. 그리고 앞에서 일정하게 불어오는 공기에게 각운동량 따위가 있을리가 없다. 어딘가를 중심으로 회전해야 각운동량이 생기기 때문이다.[각주:3] 뭐 일단 자세한 설명은 생략하고, 실제 물체가 있는 곳 주위를 제외한 다른 부분에서는 대부분 vorticity가 0이다. 이런 부분을 따라 contour를 그리는 것이다. 그런데 비행기가 뜨기 위해서는 lift가 존재해야 하고, 위의 정리를 따르면 circulation이 0이면 안된다. 그런데도 velocity potential 자체는 정의할 수 있다. magnetic scalar potential과 비슷한 개념이라고 생각하면 될 듯 하다.[각주:4] 당연히 이 녀석은 Riemann surface 비슷하게 한 지점에서 하나의 값만 정의되지는 않는다. complex variable analysis에서 residue와 비슷하다고 해야 하나?

잡담은 여기까지 하고(무언가 헤맨 느낌이 들지만), 직접 증명해보자. 일반적으로는 complex potential을 이용한다고 하는데, 그런 고등한 방식은 우리에게 어울리지 않는다.(이 방법으로 증명한 것을 보고 싶으면 여기로) 좀 더 바로 바로 와 닿는 증명은 없을까? 구멍이 조금 있어 엄밀하지는 못하지만(메꿀 수는 있는 구멍이다.) 이런 방식으로 증명하는 것도 가능하다.

대충 다음처럼 airfoil 하나를 준다. Kutta조건을 만족하려면 아래처럼 흐르게 된다.


이전 글에서 긁어왔던 그림. 이번에도 여기에서

circulation이 생겼다. 그러면 이제 이 airfoil이 하나의 점처럼 보일 때까지 시야를 확대한다.

대충 이런 느낌이다.

이제 중요한 부분. 이렇게 매우 먼 지점에서 유체의 y방향 운동량 성분의 변화를 분석한다. 먼저 r이 매우 커지면 가장 중요한 성분은 다음 세 가지가 된다.

\text{at large } r\gg1\text{, flow field is characterized by}\\\\ \begin{array}{cc} \text{flow from infinity}&V_\infty\hat x\\ \text{source flow}&\frac\Lambda{2\pi r}\hat r\\ \text{vortex flow}&-\frac\Gamma{2\pi r} \hat\theta \end{array}\\\\ \text{on the first order of } \frac1r

r의 -1차항까지 분석하는 이유는 우리가 적분할 때 r의 order를 갖는 weighting factor를 부여할 것이기 때문이다. 일단 확실한 것은 airfoil이 있어도 유체가 새로 생성되거나 사라지지는 않는다는 것이다.

\Lambda=0

먼저 들어오는 y 운동량을 측정하자. 일단 다음과 같이 그림을 잡으면 미소시간 dt동안 들어온 y방향 성분을 알 수 있다.


a>>1으로 두기 때문에 위에서 얻은 근사식을 적용한다. 흘러 들어오는 질량은 수직길이당 \rho_\infty V_\infty dt 이므로 적분은 대충 다음처럼 생겼다.

p_{y,i}=\int_\infty^\infty \rho_\infty V_\infty dt\frac\Gamma{2\pi r}\cos\theta dl~~~~~~~~~~~~~~~~~\\ =\int_\infty^\infty \rho_\infty V_\infty dt\frac\Gamma{2\pi a\sec\theta}\cos\theta~ d(a\tan\theta)\\ =\int_{-\pi/2}^{\pi/2} \rho_\infty V_\infty dt\frac\Gamma{2\pi}d\theta\\ =\frac12\rho_\infty V_\infty \Gamma dt

뒷쪽에 대해서도 같은 식을 구할 수 있다. 다만 이 때는 vortex가 유도한 y성분의 속도 방향이 아래쪽이므로,

p_{y,o}=-\frac12\rho_\infty V_\infty dt

이다. 따라서 airfoil이 전체 유동장에 주는 힘은

\text{momentum transferred into the fluid flow} = p_{y,o}-p_{y,i}\\ =-\rho_\infty V_\infty\Gamma dt\\\\ \therefore \text{force transferred into the fluid flow}={p_{y,o}-p_{y,i}\over dt}\\ =-\rho_\infty V_\infty\Gamma

이제 뉴턴 3법칙을 이용한다.

\text{lift} = -\text{force transferred into the fluid flow}\\\\ \therefore L'=\rho_\infty V_\infty\Gamma~~~~~~~~~~~~~~~~~

증명 완료. 이런 방식으로 증명하게 되면 Navier-Stokes 방정식처럼 potential flow를 가정할 수 없는 경우에도 Kutta-Joukowski 정리가 대략적으로 성립한다는 것을 보여줄 수 있을지도 모른다는 생각이 들었지만 생각해보면 점성때문에 r의 -1차 항이 0으로 배는 빠르게 수렴하는구나. 교수님께서는 이 식이 점성이 있어도 대충 맞는다고 하셨는데 그렇게 잘 맞게 하려면 어떻게 contour를 잡는지에 대한 감각이 필요할 것 같다.

쓰고 나서 보니 막쓴 항들이 보이는데 너그러운 마음으로 무시해 주시길 바란다, 정 찝찝하면 dt를 Δt로 바꾸시면 되겠다.
  1. 전자기에서 주로 만나서 몰랐는데, 이 인물이 원래는 유체역학을 하던 사람이라고 한다. 교수님 말씀하시길: "천재는 무언가 하면 이곳저곳에 흔적을 남기는 법이야"(맞나?) [본문으로]
  2. 2차원이다. 3차원이 아닌 공간에서 curl을 쓰는 것이 이상하기는 하지만, z축을 임의로 도입하고 z방향의 변화는 항상 0이 된다고 가정하면 된다. [본문으로]
  3. 물론 각운동량이 존재해도 어딘가 중심을 가지고 회전하지는 않는 것처럼 보일 때가 있다. [본문으로]
  4. 비록 전자기 시간에 '이런게 있음 ㅇㅇ'하고 대충 넘어가신 것 같기는 하지만. [본문으로]
저작자표시 비영리 변경금지

'Physics > Speculations' 카테고리의 다른 글

Electromagnetism in Schrodinger Eqn.  (1) 2010.09.20
어는점내림 상수 구하기, 보론  (0) 2010.09.03
Thin airfoil theory의 결과물에 대해서(flat plate)  (2) 2010.04.24
양자역학의 유래  (4) 2010.01.19
복소수의 필연성  (0) 2010.01.19
Posted by 덱스터

2010. 4. 24. 03:09 Physics/Speculations

Thin airfoil theory의 결과물에 대해서(flat plate)

Thin airfoil theory는 말 그대로 날개가 얇다고 가정을 한 상태에서 날개 주변의 유동에 대해 해석적인(analytic) 해를 구하는 것이다. 상당히 극단적인 가정이 많이 들어가기는 하지만 의외로 잘 맞아서(실험 데이터와 오차범위를 비교해놓은 것을 보면 정확하다는 말만 나온다.) 이전에 공학과 흑묘백묘론이라는 글을 쓰는 모티브가 되기도 했다. 물론 모티브는 내 엉망인 글 솜씨에 의해서 망해버렸지만.

근사를 하는 과정은 다음과 같다.

1. 점성항을 제거한다.
Navier-Stokes 공식을 Euler 공식으로 바꾸는 것이다. 이렇게 공식을 바꾸어주면 그나마 풀 수 있는 문제로 바뀌게 된다.[각주:1]

2. 회전하지 않는다고 가정한다.
속도 벡터장의 회전도(curl)를 항등적으로 0으로 취급한다는 뜻이다. 1번과 함께 이 조건이 만족되면 속도를 스칼라 함수의 물매(gradient)로 쓸 수 있다고 해서 potential flow라고 부른다. 컴퓨터 없이 유체역학을 공부하게 되면 이런 종류의 흐름만 배울 것이다.

3. 날개를 camber만 남긴다.
camber는 날개의 윗 단면과 날개의 아랫 단면의 정중앙을 지나는 곡선이다. 임의의 수직선을 생각했을 때 camber가 날개를 정확히 반으로 가른다고 생각해도 좋고, 윗 단면과 아랫 단면의 평균이라고 생각해도 좋다. 중요한 것은 날개에 이 녀석만 남겨서 두께를 0으로 만들어 버린다는 것이다.

4. x축에 vortex를 적절히 배치한다.[각주:2]
말 그대로 적절히 배치한다. 이 배치를 잘 조절해서 camber만 남긴 날개와 유체의 흐름이 평행하도록 만들어주는 것이다. 비행기가 날 때 공기가 날개를 뚫고 흐르지는 않는 것을 모사한다.

정확한 것은 책을 찾아보세요. 블로그는 언제까지나 블로그이다.

문제는 결국 이 방정식으로 줄어들게 된다. gamma는 x축 위의 vortex 분포, V는 무한지점에서 불어오는 속도(그래서 아래첨자가 무한대이다), alpha는 받음각(angle of attack), x는 좌표, z는 camber의 공식. 0에서부터 c까지 적분한다는 소리는 날개의 앞쪽 끝에서 뒤쪽 끝까지 적분한다는 의미이다.

\frac1{2\pi}\int_{0}^{c}\frac{\gamma(\xi)d\xi}{x-\xi}=V_\infty\left(\alpha-\frac{dz}{dx}\right)

Anderson의 Fundamentals of Aerodynamics 4th Ed.을 쓰고 있는데, 여기서는 날개를 완전히 평평한 판으로 근사했을 때(dz/dx=0)의 해를 다음과 같이 구해놓았다.

\gamma(\theta)=2\alpha V_\infty\frac{1+\cos(\theta)}{\sin(\theta)}\\x=\frac{c}2(1-\cos(\theta))

재미있는 것은 이 식이 경험법칙인 Kutta condition을 만족한다는 사실이다. Kutta 조건은 어떤 실험을 해 보아도 날개 끝 지점에서 유체의 움직임은 끝의 생김새와 평행하다는 것이다. 수식으로 바꾸면 gamma가 날개의 끝 지점에서는 0이라는 말이다.



아래 그림이 Kutta 조건을 만족할 때의 유동 모습이다. 일단 책에 나온 해의 그래프는 다음과 같이 그려진다.

c를 1로 잡았다. y축은 어차피 분포를 보여주기 위한 목적이 전부이니 무시.

자, 어떻게 다음 적분방정식(integral equation)의 해가 저렇게 깔끔한 성질을 보여줄까?

\frac1{2\pi}\int_{0}^{c}\frac{\gamma(\xi)d\xi}{x-\xi}=V_\infty\alpha

결론부터 말하자면, 당연히 깔끔할 수 밖에 없다. 일반적으로 적분방정식의 해는 여러개가 나오는데 그 중에서 우리가 원하는 조건에 맞는 녀석만 남도록 경계조건(boundary condition)을 적용했기 때문이다.[각주:3] 방정식 자체는 alpha와 V의 부호를 동시에 바꾸어도 동일하다는 점에 주목하길 바란다. 이 말은 위에서 구한 분포가 반대 방향에서 불어오고 있을 때에도 유효한 답이 된다는 말과 똑같은 소리이다.

\frac1{2\pi}\int_{0}^{c}\frac{\gamma(\xi)d\xi}{x-\xi}=(-V_\infty)(-\alpha)
의 해도\gamma(\theta)=2\alpha V_\infty\frac{1-\cos(\theta)}{\sin(\theta)}\\x=\frac{c}2(1-\cos(\theta))
가 된다.


다르게 표현한다면 다음 해도 사실은 유효하다는 것이다.부호 반대.

\gamma(\theta)=2\alpha V_\infty\frac{1-\cos(\theta)}{\sin(\theta)}\\x=\frac{c}2(1-\cos(\theta))

하늘색이 새로운 해의 분포

그래서 수업시간에 교수님께서 질문하신 "왜 답이 이렇게 깔끔한지 알기나 하냐?"에 대한 답은 "깔끔하도록 제한해주었으니까요"가 되겠다.


2012.11.14
좌우 대칭으로 바꾸어주면서 gamma의 부호도 바꾸어주어야 하는데 그 부분이 빠졌다.(시계방향 회전을 좌우대칭으로 바꾸면 반시계방향 회전이 된다.) 따라서 실제 위의 방정식을 만족하는 해는 다음 식이 된다.


\gamma(\theta)=2\alpha V_\infty\frac{\cos(\theta)-1}{\sin(\theta)}\\x=\frac{c}2(1-\cos(\theta))


양력은 음수가 되는 것을 알 수 있다. 전혀 쓰일 이유가 없는 해인 것이다.


  1. N-S 방정식을 완전히 풀어낸 해는 모두 합쳐도 손으로 꼽을 수 있을 정도밖에는 안된다. 그 중 하나가 원통 내부를 흘러가는 유체의 유동방정식인데, 이 녀석도 유체가 안정적으로(laminar) 흐를 때에만 유용한 녀석이라 좀 문제가 있다. 수도꼭지에서 물을 틀면 물이 매끈한 원기둥처럼 나올 때가 있고 이곳 저곳 울퉁불퉁한 흐름이 생기는 경우도 있는데 후자가 근처에서 가장 쉽게 관찰할 수 있는 불안정한(turbulent) 경우이다. 그나마 제대로 푼 식이라도 제한적으로만 의미가 있다는 뜻이다. CFD(Computational Fluid Dynamics)가 발전한 이유이기도 하고. [본문으로]
  2. 전자기학에 비유한다면, 적절한 전하밀도를 분포시키는 것이다. [본문으로]
  3. 양자역학의 산란 파트에서 Born approximation을 할 때에도 적분방정식을 푼다. 이때 나오는 독립적인 해가 두개인가 되는데, 그 중 하나는 경계조건으로 날려버린다. [본문으로]
저작자표시 비영리 변경금지

'Physics > Speculations' 카테고리의 다른 글

어는점내림 상수 구하기, 보론  (0) 2010.09.03
Kutta-Joukowski Theorem, alternate proof(without residue theorem)  (4) 2010.05.30
양자역학의 유래  (4) 2010.01.19
복소수의 필연성  (0) 2010.01.19
운동량 연산자에 대해서(1)  (7) 2009.12.14
Posted by 덱스터
이전버튼 1 이전버튼
블로그 이미지
A theorist takes on the world
덱스터
Yesterday
Today
Total

달력

 « |  » 2024.11
일 월 화 수 목 금 토
1 2
3 4 5 6 7 8 9
10 11 12 13 14 15 16
17 18 19 20 21 22 23
24 25 26 27 28 29 30

최근에 올라온 글

최근에 달린 댓글

글 보관함

티스토리툴바