2009. 12. 14. 23:41 Physics/Speculations
운동량 연산자에 대해서(1)
양자물리를 Griffith 책으로 공부하다 보면 나타나는 의문이 참 많다. 그 중에서 내가 가장 큰 의문을 가졌던 것은 운동량 연산자에 대한 것이었다. 어째서 운동량 연산자는 x로 span된 힐베르트 공간에서 미분으로 나타나는 것일까?
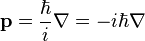
그 이름이 암시하듯이, 운동량이란 물체의 운동 즉 시간과는 떼어놓고 생각할 수 없는 존재이다. 그런데 어째서 운동량을 나타내는 연산자는 시간에 무관한 것일까?
맨 처음 운동량 연산자를 유도해내는 과정을 보고서 내가 느낀 것은, '운동량에 대응하는 정보가 파동함수에 들어 있고, 그 정보는 어떤 연산을 통해서 외부에 나타난다. 따라서, 운동량의 고전적인 정의를 이용해서 운동량에 해당하는 연산자를 유도해내는 것은 아닐까?'였다.
하지만 문제는, 우리가 알고 있는 Schrodinger 방정식 자체가 운동량 연산자를 가정하는 것에서 출발했다는 것이다. 보통 Schrodinger 방정식은 다음과 같은 형태로 쓴다.
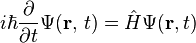
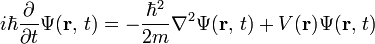
H는 Hamiltonian 연산자로, 고전역학에서 사용하는 Hamiltonian이라는 물리량에 해당한다. 일반적인 경우, Hamiltonian은 계 전체의 에너지와 같은 값을 갖는다. 따라서, Schrodinger 방정식은 계를 나타내는 상태함수가 에너지에 비례하여 시간적으로 변화한다는 것을 나타낸다고 볼 수 있다. 그리고 고전적으로 운동에너지는 운동량의 제곱을 질량의 두배로 나눈 값이다. Schrodinger 방정식의 첫 항(Laplacian이 들어가 있는 항)을 잘 보면 바로 앞서 구한 운동량의 제곱을 질량의 두배로 나눈 값, 즉 고전적인 운동에너지라는 것을 알 수 있다. 결국, 우리는 원점으로 돌아온 것이다.2 그렇다면 어떻게 해야 운동량에 해당하는 연산자를 구할 수 있을까?
쓰기 귀찮아서 여기까지만...(여기까지 써놓고 끝날 가능성도 농후)
관심이 가시는 분은 여기를 참조:
http://en.wikipedia.org/wiki/Schr%C3%B6dinger_equation#Derivation
Erwin Schrodinger의 원본을 보고 싶으신 분을 위하여:
http://home.tiscali.nl/physis/HistoricPaper/Schroedinger/Schroedinger1926c.pdf
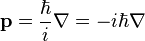
3차원 공간에서 운동량 연산자. Wikipedia: Momentum operator
그 이름이 암시하듯이, 운동량이란 물체의 운동 즉 시간과는 떼어놓고 생각할 수 없는 존재이다. 그런데 어째서 운동량을 나타내는 연산자는 시간에 무관한 것일까?
맨 처음 운동량 연산자를 유도해내는 과정을 보고서 내가 느낀 것은, '운동량에 대응하는 정보가 파동함수에 들어 있고, 그 정보는 어떤 연산을 통해서 외부에 나타난다. 따라서, 운동량의 고전적인 정의를 이용해서 운동량에 해당하는 연산자를 유도해내는 것은 아닐까?'였다.
1. 어떤 연산이 있어 운동량에 대응된다.
2. 고전적인 운동량에 해당하는 값은 다음과 같다.
3. 이미 알려진 Schrodinger 방정식을 적절히 손보면, 다음 식을 얻는다.1
4. 여기서 운동량에 해당하는 연산을 찾을 수 있다.(연산자를 강조하기 위해 ^ 사용)
\langle{p}\rangle=\int\psi^{\star}{p}\psi{dx}2. 고전적인 운동량에 해당하는 값은 다음과 같다.
p_{classical}=m\frac{d}{dt}\langle{x}\rangle=m\frac{d}{dt}\int\psi^\star{x}\psi{dx}3. 이미 알려진 Schrodinger 방정식을 적절히 손보면, 다음 식을 얻는다.1
m\frac{d}{dt}\int\psi^\star{x}\psi{dx}=\int\psi^\star{\frac{\hbar}{i}\frac{d}{dx}}\psi{dx}4. 여기서 운동량에 해당하는 연산을 찾을 수 있다.(연산자를 강조하기 위해 ^ 사용)
\hat{p}=\frac{\hbar}{i}\frac{d}{dx}하지만 문제는, 우리가 알고 있는 Schrodinger 방정식 자체가 운동량 연산자를 가정하는 것에서 출발했다는 것이다. 보통 Schrodinger 방정식은 다음과 같은 형태로 쓴다.
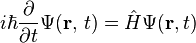
하나의 계에 대한 Schrodinger 방정식
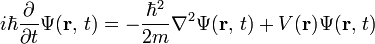
입자 하나에 대한 Schrodinger 방정식. Wikipedia: Schrodinger equation
H는 Hamiltonian 연산자로, 고전역학에서 사용하는 Hamiltonian이라는 물리량에 해당한다. 일반적인 경우, Hamiltonian은 계 전체의 에너지와 같은 값을 갖는다. 따라서, Schrodinger 방정식은 계를 나타내는 상태함수가 에너지에 비례하여 시간적으로 변화한다는 것을 나타낸다고 볼 수 있다. 그리고 고전적으로 운동에너지는 운동량의 제곱을 질량의 두배로 나눈 값이다. Schrodinger 방정식의 첫 항(Laplacian이 들어가 있는 항)을 잘 보면 바로 앞서 구한 운동량의 제곱을 질량의 두배로 나눈 값, 즉 고전적인 운동에너지라는 것을 알 수 있다. 결국, 우리는 원점으로 돌아온 것이다.2 그렇다면 어떻게 해야 운동량에 해당하는 연산자를 구할 수 있을까?
쓰기 귀찮아서 여기까지만...(여기까지 써놓고 끝날 가능성도 농후)
관심이 가시는 분은 여기를 참조:
http://en.wikipedia.org/wiki/Schr%C3%B6dinger_equation#Derivation
Erwin Schrodinger의 원본을 보고 싶으신 분을 위하여:
http://home.tiscali.nl/physis/HistoricPaper/Schroedinger/Schroedinger1926c.pdf
'Physics > Speculations' 카테고리의 다른 글
| 양자역학의 유래 (4) | 2010.01.19 |
|---|---|
| 복소수의 필연성 (0) | 2010.01.19 |
| 요즘 하는 생각 (0) | 2009.12.04 |
| Time operator? (2) | 2009.10.20 |
| 왜 하필이면 Hamiltonian 연산자인가? (0) | 2009.10.17 |


