2014. 1. 11. 03:12 Mathematics
Poincare Half Plane 푸앙카레 반평면 (1)
일반상대론 교재를 보고 식은 이해했는데 실제 연습문제를 풀 때마다 막막하신 분들을 위해 적습니다.
많은 이들을 멘붕에 빠지게 하는 일반상대론이 어려운 이유는 다른게 아니라 일반상대론에서 사용하는 리만기하학 때문입니다. 유클리드 공간에서 작도만 하던 그리스 시대와는 달리 시간이 지날수록 사람들은 '두 점 사이의 거리'에도 관심을 갖게 됩니다. 두 점 사이의 거리는 피타고라스의 정리로 쓰게 되죠.
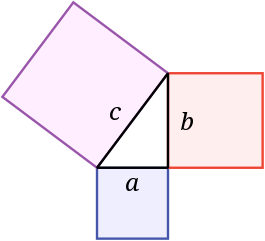
c^2=a^2+b^2
이런 '두 점 사이의 거리'를 재는 방법을 가장 간단하게 일반화한 것이 리만기하입니다. 매우 가까운 두 점 사이의 거리는 두 점과 좌표축에 평행한 선분이 만드는 삼각형(편의상 2차원이라고 합시다)의 각 변의 길이에 대한 이차식의 꼴로 나타난다는 것이죠. 원래는 가우스가 휘어진 곡면 위에서 두 점 사이의 거리는 어떻게 주어지는가를 연구하면서 등장하게 되었다고 하는군요.
ds^2=Edx^2+2Fdxdy+Gdy^2
사실 거리를 일반화하는 방법은 이것 말고도 더 많기에 -피타고라스 정리에 제곱 대신 네제곱을 쓸 수도 있는 것이니까요. 페르마 님이 좋아합니다- 제곱의 꼴로 거리가 주어지는 리만기하학의 공간을 L^2공간이라고도 부릅니다. 양자역학에서 사용하는 힐베르트 공간도 L^2 공간의 일종이죠. 여기에 대해서는 아는 것의 밑천이 바닥나지 않을 이 정도 까지만 썰을 풀기로 합시다(...).
리만기하가 얼마나 일반적인 상식(?)과 어긋나는지 보기 위해 구체적인 문제를 풀어보도록 합시다. 가장 간단한 문제는 아무래도 푸앙카레 반평면(Poincare Half Plane)이 되겠네요. 푸앙카레 반평면이란 매우 가까운 두 점 사이의 거리 ds를 다음과 같이 정의하는 공간입니다.
ds^2=\frac{1}{y^2}(dx^2+dy^2)
여기서 리만기하학을 처음부터 다룰 수는 없는 노릇이니, 근처에 미분기하학 책이 하나 정도는 있다고 가정하고 바로 geodesic equation을 푸는 것으로 들어가도록 하겠습니다. 아무 일반상대론 책 하나 펴고 geodesic equation을 구하는 증명과정을 쭉 풀어본 사람이라도 실제 geodesic이 무엇이냐를 푸는데는 어려움을 겪는 경우가 있어서요. 그러면 방정식을 풀어봅시다.
geodesic equation은 다음과 같이 씁니다.
\frac{d^2x^\mu}{d\lambda^2}+\Gamma^\mu_{\alpha\beta}\frac{dx^\alpha}{d\lambda}\frac{dx^\beta}{d\lambda}=0
단, 이 경우 이 식이 만족되어야 합니다. 상수는 보통 1로 많이 잡는데, 그러면 람다의 변화는 이동한 거리가 되죠.
\frac{dx^\mu}{d\lambda}\frac{dx_\mu}{d\lambda}=\text{const}
위의 metric을 이용해서 connection coefficient(혹은 Christoffel symbol이라고도 부릅니다)를 구하면 다음과 같습니다. (summation은 그리스 문자만 해당하는 것으로 합시다)
\Gamma^x_{xy}=\Gamma^y_{yy}=-\Gamma^y_{xx}=-\frac1y
위로부터 다음 식을 계산해보면 이 식이 맞다는 것도 확인할 수 있죠.
\Gamma^\mu_{\mu\nu}=\partial_\nu\ln\sqrt{|g|}
람다에 대한 미분을 뉴턴식으로 간략하게 쓰기로 하면 geodesic equation은 다음과 같이 정리할 수 있습니다.
y''+\frac1y(x'^2-y'^2)=x''-\frac{2x'y'}y=0
확인한다면 위 식의 하나는 다음과 같이 쓸 수 있다는 것을 보일 수 있지요.
y^2\left(\frac{x'}{y^2} \right )'=0 \;\;\cdots\;x'=\alpha y^2
여기서 첫번째 geodesic을 얻습니다. 알파를 0으로 두면 geodesic은 x=const가 되거든요. 그러면 이 경우를 무시한 채 계속 진행해봅시다. 위에서 얻은 관계식을 대입하면 되는데, 우선은 어려운 방법부터 해 보도록 합시다.1 남은 geodesic equation에 위 관계식을 대입하면 다음 식을 얻습니다.
y''+\frac1y(\alpha^2y^4-y'^2)=y\left[(\ln y)''+\alpha^2y^2 \right ]=0
y의 로그를 z로 재정의하면 다음 식을 얻죠. 신나게 미분방정식을 풀어봅니다.
z\equiv\ln y
\\z''+\alpha^2e^{2z}=0\;\;\cdots\;\;2z'z''+2\alpha^2e^{2z}z'=\left[z'^2+\alpha^2e^{2z}\right ]'=0
\\z'^2+\alpha^2e^{2z}=\frac{y'^2}{y^2}+\alpha^2y^2=\beta^2\;\;\cdots\;\;y'=\beta{y}\sqrt{1-\left(\frac{\alpha y}{\beta} \right )^2}
\\\therefore\frac{dy}{y\sqrt{1-\alpha^2y^2}}=d\lambda\;\;\;\cdots\;\beta\text{ is considered }1
베타는 어차피 중요한 상수가 아니라서 그냥 1로 두었습니다. 나중에 끌고가 보시면 알겠지만 베타는 속도에 해당합니다. 그리고 마지막 적분은 매우 유명(?)한 적분입니다. 저런 꼴은 일단 삼각함수로 치환하고 생각합니다.
y\equiv\frac{\sin\chi}{\alpha}
\\\frac{d\chi}{\sin\chi}=d\lambda\;\;\cdots\;\;\lambda=\ln\left(\frac{\sin\chi}{1+\cos\chi} \right )
\\\therefore e^\lambda=\frac{\alpha y}{1+\sqrt{1-\alpha^2y^2}}\;\;\cdots\;\;e^\lambda\sqrt{1-\alpha^2y^2}=\alpha y-e^\lambda
\\\therefore y=\frac1\alpha\;\text{sech }\lambda
참 쉽죠?(...) 마지막 줄은 그냥 전 줄을 제곱한 뒤 슥슥 그어주면 얻습니다. y를 구했으니 이번엔 x를 구할 차례로군요.
x'=\alpha y^2=\frac1\alpha\;\text{sech}^2\;\lambda\;\;\cdots\;\;x=x_0+\frac1\alpha\;\text{tanh}\;\lambda
\\\therefore (x-x_0)^2+y^2=\frac{1}{\alpha^2}
위를 종합하면 geodesic은 원으로 그려지게 됩니다. 물론 '우리 눈으로 보기에 원'이지, 실제 원은 아니지요. 원은 '한 점으로부터 등거리에 있는 점의 집합'이니까요.
이제 미분방정식을 푸는 쉬운 방법을 알려드리죠. 아까 구한 관계식을 이번에는 속도의 크기에 넣어줍니다.
\frac{1}{y^2}\left(x'^2+y'^2 \right )=\frac{1}{y^2}\left(\alpha^2y^4+y'^2 \right )=1
\\\therefore y'^2=y^2(1-\alpha^2y^2)\;\;\cdots\;\;y'=y\sqrt{1-\alpha^2y^2}
어라(...) 힘들게 z로 치환해가며 구했던 미분방정식을 얻었습니다. 실제로 이 식을 미분해서 정리하면 사용하지 않은 geodesic equation으로 정리되는 것을 알 수 있습니다.
geodesic을 구했으니 남은건 '임의의 두 점 사이의 거리'같은 것이 있겠지만 그런거나 하자고(...) 이 글을 쓰고 있는 것은 아니죠. 다음 글을 쓰게 된다면 그 때는 푸앙카레 반평면을 비틀어 보도록 하겠습니다. 일종의 반-푸앙카레 반평면(Anti-Poincare Half Plane) 혹은 민코프스키 푸앙카레 반평면(Minkowskian Poincare Half Plane)이라고 할 수 있죠.
ds^2=\frac{1}{z^2}(-dt^2+dz^2)
이런 metric을 생각한 이유는 de Sitter 공간과 Anti-de Sitter 공간을 단순화하면 이런 꼴의 metric으로 쓸 수 있기 때문이었죠. 혹시 시간이 되시는 분들은 괜찮은 일반상대론 책에서 conformal transformation을 찾아본 뒤 다음 metric의 scalar curvature를 계산해보세요. 모든 공간에서 상수가 나옵니다.
\\ds^2=\frac{1}{t^2}(-dt^2+dx^2+dy^2+dz^2)\;\;\cdots\text{de Sitter}
\\
\\ds^2=\frac{1}{z^2}(-dt^2+dx^2+dy^2+dz^2)\;\;\cdots\text{Anti-de Sitter}
그러면 다음 시간에(그런게 있다면)...
- 제가 처음 푼 방법인데 지금 이 풀이를 보면 정신이 아득하네요. 내가 이렇게 머리가 쌩쌩 돌아갔던가... [본문으로]
'Mathematics' 카테고리의 다른 글
| Commutators in finite dimensions and identity matrix (0) | 2014.08.15 |
|---|---|
| Poincare Half Plane 푸앙카레 반평면 (2) (0) | 2014.05.25 |
| Continuously Updated Fourier Series (0) | 2013.12.06 |
| 개드립의 마지막 정리 (0) | 2013.10.29 |
| 델타 분포 만들기 (6) | 2012.08.23 |


