2010. 2. 24. 23:47 Mathematics
야코비 행렬(Jacobian matrix)
처음 야코비 행렬을 보았을 때는 아마도 신입생 시절이었을 것이다.(기껏해야 재작년이지만) 야코비 행렬의 정의는 wikipedia 항목을 뒤져보면 쉽게 찾을 수 있다.

$$d\mathbf F=\mathbf Jd\mathbf r$$
의문이 생기면 직접 확인해 보도록. 벡터의 각 성분을 스칼라함수로 본 상태에서 기울기를 구해 행벡터로 나열하고, 여기에 뒤쪽의 미소변위 벡터를 곱하면 각 항목마다 내적을 취하게 되어서 그렇다.2

위 링크에서는 n차원 유클리드 공간에서 m차원 유클리드 공간으로 보내는 사상 F에 대해서 정의되는 값이라고 되어있다. 다른 말로 하자면 n개의 x 성분이 있는 공간에서 정의된 m개의 y 성분이 있는 벡터장(vector field) F의 기울기(gradient)라고도 할 수 있다. 먼저 기울기의 성격을 잘 생각해보자.
$$d\psi=\nabla\psi\cdot d\mathbf r$$
위 식은 장을 측정하는 위치가 조금 변했을 때 장의 크기가 변하는 정도는 그 위치변화(변위)와 장의 기울기의 내적과 같다는 것을 말해주고 있다. 벡터장의 경우 동일한 결론을 얻게 되는데, 물론 벡터를 열벡터로 쓰는 것에 동의한 경우이다.1 야코비 행렬을 J라고 쓰면 미소변위 dr만큼 움직였을 때 벡터장 F의 변화 dF는 다음과 같다.
의문이 생기면 직접 확인해 보도록. 벡터의 각 성분을 스칼라함수로 본 상태에서 기울기를 구해 행벡터로 나열하고, 여기에 뒤쪽의 미소변위 벡터를 곱하면 각 항목마다 내적을 취하게 되어서 그렇다.2
이 행렬의 행렬식(determinant)은 상당히 자주 이용된다. 물론 행렬식을 이용하려면 사상이 같은 차원의 공간을 이어주어야 한다. 대표적인 예는 구면좌표계를 직교좌표계로 바꾸는 경우가 있다. wikipedia의 동일 항목에 나온 예이긴 하지만,3 이보다 적절한 예는 없다고 생각해서 이 예를 쓰도록 하겠다.

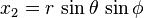

이 경우의 야코비 행렬은
![J_F(r,\theta,\phi) =\begin{bmatrix}
\dfrac{\partial x_1}{\partial r} & \dfrac{\partial x_1}{\partial \theta} & \dfrac{\partial x_1}{\partial \phi} \\[3pt]
\dfrac{\partial x_2}{\partial r} & \dfrac{\partial x_2}{\partial \theta} & \dfrac{\partial x_2}{\partial \phi} \\[3pt]
\dfrac{\partial x_3}{\partial r} & \dfrac{\partial x_3}{\partial \theta} & \dfrac{\partial x_3}{\partial \phi} \\
\end{bmatrix}=\begin{bmatrix}
\sin\theta\, \cos\phi & r\, \cos\theta\, \cos\phi & -r\, \sin\theta\, \sin\phi \\
\sin\theta\, \sin\phi & r\, \cos\theta\, \sin\phi & r\, \sin\theta\, \cos\phi \\
\cos\theta & -r\, \sin\theta & 0
\end{bmatrix}.](http://upload.wikimedia.org/math/d/7/9/d791528200a6f3c81162837ca9624f39.png)
이 된다. 위 링크를 따라가보면 알겠지만 야코비 행렬식은 미소부피가 얼마나 팽창하는지 알려주는 계수가 된다. 위의 경우에서 행렬식을 구하면 r^2 sin θ가 되는데, 구면좌표계를 공부한 사람들은 알다시피 dx dy dz = r^2 sin θ dr dθ dφ 이다. 왜 그런지는 이렇게 보일 수 있다. 편의상 야코비 행렬이 다음과 같은 모습이라고 하자.
이제는 다음 방정식이 성립한다.
아까의 예제대로라면 x는 데카르트 좌표계, y는 구면좌표계의 미소변화이다. 위 식을 풀어쓰면 다음과 같은 세 방정식이 된다.
이제 미소부피를 구할 차례이다. 그런데 애석하게도, 미소부피는 저 세 값을 단순히 곱한다고 얻어지는게 아니다. 잘 생각해보면 각 항목은 하나의 벡터이다. 따라서 단위벡터를 ^를 씌워 나타낸다면 위 방정식은 정확히는 이런 방정식이 된다.
그리고 미소부피를 정확히 나타내려면 위 세 벡터를 스칼라곱 해주어야 한다. 더 높은 차원에서는 쐐기곱을 해주어야 하는데, 아직은 필요없으니 무시하자. 더 알고 싶은 사람은 여기를 확인하고, 여기서는 계속 나아가도록 하겠다. 이제 미소부피 dV는 다음과 같이 쓸 수 있다.
삼중곱을 간단히 나타내는 방법을 우리는 아주 잘 알고있다. 행렬식을 이용하는 것. y를 사용하는 공간도 유클리드 공간이기 때문에 각 벡터를 성분으로만 써주면 이렇게 된다.
이제 삼중곱.
행렬식의 성질때문에 같은 열에 곱해진 숫자는 앞으로 튀어나올 수 있다. dy_1등을 행렬에서 제거해주자.
이제 사실상 의미없는 삼중곱을 지워주면 우리가 그토록 애타게 원하던 결과가 나온다.
강의를 듣던 당시에는 '오 신기하네' 정도로 생각하고 넘어갔는데 돌이켜보니 나름대로의 논리가 스며들어 있었던 결과물중 하나이다. 설명을 다시 짚어보지 않아서 제대로 설명했는지는 모르겠다.

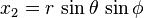

이 경우의 야코비 행렬은
![J_F(r,\theta,\phi) =\begin{bmatrix}
\dfrac{\partial x_1}{\partial r} & \dfrac{\partial x_1}{\partial \theta} & \dfrac{\partial x_1}{\partial \phi} \\[3pt]
\dfrac{\partial x_2}{\partial r} & \dfrac{\partial x_2}{\partial \theta} & \dfrac{\partial x_2}{\partial \phi} \\[3pt]
\dfrac{\partial x_3}{\partial r} & \dfrac{\partial x_3}{\partial \theta} & \dfrac{\partial x_3}{\partial \phi} \\
\end{bmatrix}=\begin{bmatrix}
\sin\theta\, \cos\phi & r\, \cos\theta\, \cos\phi & -r\, \sin\theta\, \sin\phi \\
\sin\theta\, \sin\phi & r\, \cos\theta\, \sin\phi & r\, \sin\theta\, \cos\phi \\
\cos\theta & -r\, \sin\theta & 0
\end{bmatrix}.](http://upload.wikimedia.org/math/d/7/9/d791528200a6f3c81162837ca9624f39.png)
이 된다. 위 링크를 따라가보면 알겠지만 야코비 행렬식은 미소부피가 얼마나 팽창하는지 알려주는 계수가 된다. 위의 경우에서 행렬식을 구하면 r^2 sin θ가 되는데, 구면좌표계를 공부한 사람들은 알다시피 dx dy dz = r^2 sin θ dr dθ dφ 이다. 왜 그런지는 이렇게 보일 수 있다. 편의상 야코비 행렬이 다음과 같은 모습이라고 하자.
$$J_F=\left(\begin{array}{ccc} a&b&c\\d&e&f\\g&h&i \end{array}\right)
$$
이제는 다음 방정식이 성립한다.
$$d\mathbf x=J_Fd\mathbf y
$$
아까의 예제대로라면 x는 데카르트 좌표계, y는 구면좌표계의 미소변화이다. 위 식을 풀어쓰면 다음과 같은 세 방정식이 된다.
$$dx_1=a~dy_1+b~dy_2+c~dy_3\\ dx_2=d~dy_1+e~dy_2+f~dy_3\\ dx_3=g~dy_1+h~dy_2+i~dy_3$$
이제 미소부피를 구할 차례이다. 그런데 애석하게도, 미소부피는 저 세 값을 단순히 곱한다고 얻어지는게 아니다. 잘 생각해보면 각 항목은 하나의 벡터이다. 따라서 단위벡터를 ^를 씌워 나타낸다면 위 방정식은 정확히는 이런 방정식이 된다.
$$dx_1\hat{x_1}=a~dy_1\hat{y_1}+b~dy_2\hat{y_2}+c~dy_3\hat{y_3}\\ dx_2\hat{x_2}=d~dy_1\hat{y_1}+e~dy_2\hat{y_2}+f~dy_3\hat{y_3}\\ dx_3\hat{x_3}=g~dy_1\hat{y_1}+h~dy_2\hat{y_2}+i~dy_3\hat{y_3}
$$
그리고 미소부피를 정확히 나타내려면 위 세 벡터를 스칼라곱 해주어야 한다. 더 높은 차원에서는 쐐기곱을 해주어야 하는데, 아직은 필요없으니 무시하자. 더 알고 싶은 사람은 여기를 확인하고, 여기서는 계속 나아가도록 하겠다. 이제 미소부피 dV는 다음과 같이 쓸 수 있다.
$$dV=(dx_1\hat{x_1})\cdot( dx_2\hat{x_2})\times (dx_3\hat{x_3})$$
삼중곱을 간단히 나타내는 방법을 우리는 아주 잘 알고있다. 행렬식을 이용하는 것. y를 사용하는 공간도 유클리드 공간이기 때문에 각 벡터를 성분으로만 써주면 이렇게 된다.
$$\mathbf{dx_1}=(a~dy_1,b~dy_2,c~dy_3)\\ \mathbf{dx_2}=(d~dy_1,e~dy_2,f~dy_3)\\ \mathbf{dx_3}=(g~dy_1,h~dy_2,i~dy_3)
$$
이제 삼중곱.
$$dV=(dx_1\hat{x_1})\cdot( dx_2\hat{x_2})\times (dx_3\hat{x_3})~~~~~~~~~~\\=\left|\begin{array}{ccc} a~dy_1&b~dy_2&c~dy_3\\d~dy_1&e~dy_2&f~dy_3\\g~dy_1&h~dy_2&i~dy_3 \end{array}\right|\hat{y_1}\cdot\hat{y_2}\times\hat{y_3} $$
행렬식의 성질때문에 같은 열에 곱해진 숫자는 앞으로 튀어나올 수 있다. dy_1등을 행렬에서 제거해주자.
$$dV=(dx_1\hat{x_1})\cdot( dx_2\hat{x_2})\times (dx_3\hat{x_3})~~~~~~~~~~\\=\left|\begin{array}{ccc} a~dy_1&b~dy_2&c~dy_3\\d~dy_1&e~dy_2&f~dy_3\\g~dy_1&h~dy_2&i~dy_3 \end{array}\right|\hat{y_1}\cdot\hat{y_2}\times\hat{y_3} \\=\left|\begin{array}{ccc} a&b&c\\d&e&f\\g&h&i \end{array}\right|dy_1~dy_2~dy_3~\hat{y_1}\cdot\hat{y_2}\times\hat{y_3}
$$
이제 사실상 의미없는 삼중곱을 지워주면 우리가 그토록 애타게 원하던 결과가 나온다.
$$dV=dx_1~dx_2~dx_3=\left|\begin{array}{ccc} a&b&c\\d&e&f\\g&h&i \end{array}\right|dy_1~dy_2~dy_3 $$
강의를 듣던 당시에는 '오 신기하네' 정도로 생각하고 넘어갔는데 돌이켜보니 나름대로의 논리가 스며들어 있었던 결과물중 하나이다. 설명을 다시 짚어보지 않아서 제대로 설명했는지는 모르겠다.
'Mathematics' 카테고리의 다른 글
| 무한대와 무한대가 만났을 때 (4) | 2010.04.13 |
|---|---|
| Power Set에 대한 잡담 (10) | 2010.03.15 |
| 선형대수와 행렬 (0) | 2010.02.04 |
| 루빅스로 배우는 군론 (0) | 2010.01.27 |
| 무한대의 비교: 자연수와 실수 (0) | 2010.01.13 |


