2013. 7. 7. 01:30 Physics/Speculations
학사졸업논문 - 자기 단극자
아쉬운 점이라면 발표 후에 깨달은 논문상의 부호 문제(...). metric을 반대로 사용해서 정의할 때 부호를 반대로 썼어야 하는 식이 몇몇 있는데다가, 중간에 Stress-energy 텐서의 부호도 잘못 썼다. 어차피 각 항이 0이 되어야 한다는 조건인지라 결론 자체는 문제가 없지만. 왜 리뷰를 봐 주신 교수님들 중 아무도 이걸 지적하지 않은걸까(...).
Kinematic Angular Momentum의 양자화는 사실 자기장이 0인 조건에서만 성립하는데 그 부분도 생략했다. 뭐, 어차피 상관없겠지.
이상민 교수님께서 리뷰하신 후 "실력도 되는데 좀 더 큰 주제를 잡지 그랬냐"는 식으로 코멘트를 달아주셨는데 워낙 오래 전부터 생각했던 주제라 그냥 썼습니다(...).
Soliton을 다루는 건 이수종 교수님을 찾아갔더니 주제를 말씀드리자 Rubakov 책을 쿨하게 던저주셔서 시작. 그걸 한 학기 내내 거의 혼자서 팠다. 올해 봄학기동안 한 일의 70%는 저거였는듯.1 그래서 봄학기에 가장 많은 스트레스의 원인이 되었던 과목이 생각보다 학점이 안 좋아서 한동안 푹 꺼져있기도 했다. 돌이켜보면 발표할 때 실수한 내 잘못이긴 하지만.
Soliton의 경우는 논문에서 사용한 좌표계에서 운동방정식을 만족하는 해를 찾으려 3주동안 손가락 한 마디 정도 되는 이면지를 써보았는데도(주로 내가 계산을 제대로 했는가 검산한거긴 하지만) 내가 사용하는 가정해(ansatz)가 해를 주지 못한다는 결론이 나와서 그냥 뒤집어서 '해가 아예 존재할 수 없음을 보여볼까?'를 시도한거다. 결과는 성공. 특정 형식을 갖는 Lagrangian들의 경우 finite energy&speed of light를 갖는 Soliton solution이 존재하지 않는다는 보다 일반적인 결론이다.
다음은 이수종 교수님을 만나서 신세계의 문(...)을 열기 전까지의 기록. 잘못 계산한 결과에서 도약했다는 것은 log 중간에 나온다. 흑역사도 잘 마무리하면 좋은 자양분이 될 수 있다는 한 사례가 되기를(...) 희망한다. '>>'로 표시된 것은 차후에 덧붙이는 주석.
이런 글이 있었다. 아직도 비슷한 생각을 하고 있는지라 자기 단극자라는 개념에 대한 회의가 주된 고민거리이다.
처음에는 자기 단극자의 Lagrangian이나 Action Integral을 구하려고 했다. 문제는 그 형식이 어떨지 아예 감이 안 잡힌다는 것. 그래서 일반적으로 사용하는 벡터 포텐셜 A를 이용하면 문제가 생기나 봤더니, 벡터 포텐셜을 사용하게 되면 gauge symmetry는 당연하다는 결론만 얻게 되었다.
한창 보고 있는 책이 장론인지라 벡터 포텐셜을 이용해서 자기 단극자가 가질 수 밖에 없는 운동방정식을 텐서 형식으로 구하려고 했는데, 그것 마져도 실패했다. 그러면서 발견한 것이, 자기 단극자는 속도가 광속보다 매우 작은 경우에조차 갈릴레이 변환을 만족할 수 없는 운동방정식을 요구한다는 것이었다. 그렇다면 역으로 자기 단극자의 운동방정식은 전혀 다른 형식, 그러니까 질량이 없어서 광속보다 매우 작은 속도 자체가 불가능한 경우라는 결론에 도착했다. 그래서 지금은 질량없는 전하의 운동방정식을 어떻게 구해야 할까 고민하고 있다. 아무래도 전하가 자기 단극자보다는 다루기 쉬우니까 말이다.
시작은 Aharanov-Bohm 효과를 자기 단극자에서는 절대로 발견할 수 없다였는데2, 어느 순간 자기 단극자의 질량은 없다로 흘러가고 있다. 만약 그렇다면 magneton보다는 magnetino라는 이름으로 불러야 하지 않을까.
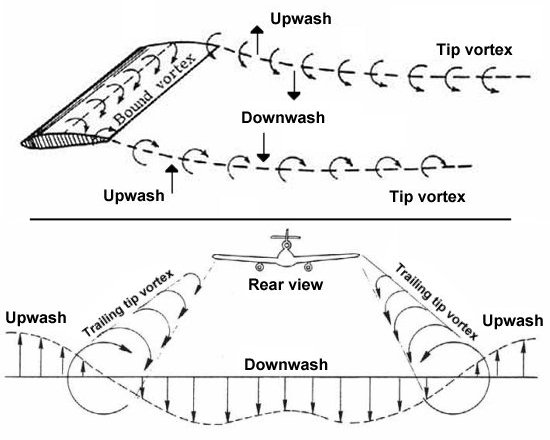
Magnetino가 유도하는 전자기장 방정식을 구했다. 로렌츠 변환 대칭성을 이용해 운동 방향에 수직한 평면에만 전자기장이 존재하도록 하면(델타함수를 이용해 자하량을 만족시킨다) 운동 방향과 같은 방향으로의 로렌츠 변환에도 변하지 않는 전자기장을 만들 수 있다.(델타함수를 재규격화하는 것이 델타함수 이외의 항에서 나타나는 상수를 상쇄시킨다.) 문제는 벡터 포텐셜. 델타함수의 역미분이 애매하다.
재미있는 것은 이렇게 구한 벡터 포텐셜이 전하와 상호작용할 경우 필연적으로 뜬금없이 각운동량이 생성되어야 한다는 것인데, 이 각운동량을 상쇄할 수 있는 것은 자하나 전하 자체에 내재된 각운동량, 즉 스핀 뿐이라는 것. 스핀은 양자화되어있기 때문에 각운동량 또한 양자화되어 있어야 하고, 따라서 전하와 자하의 곱이 양자화되어야 한다. 우연인지 항상 생성되는 각운동량 또한 전하와 자하 사이의 수직거리와는 전혀 상관이 없다. Dirac 양자화 조건과 조금 다른 듯 싶지만 비슷한 결론이라는 것이 재미있다. 졸업논문을 쓰게 되면 이걸로 쓰면 되겠네.
글을 공개로 바꾸면서 log를 다시 보니 난 수학에서나 요구할 법 한 논리적 엄밀성을 추구하는 별로 좋지 않은 버릇이 있는지도 모르겠다. 과감한 일반화가 물리의 미덕인데...
'Physics > Speculations' 카테고리의 다른 글
| 레이저로 가열할 수 있는 최대 온도에 대하여 (1) | 2013.10.18 |
|---|---|
| Cyanide 흡수스펙트럼 (0) | 2013.08.21 |
| 양자역학의 유래(2) (0) | 2012.11.08 |
| Electromagnetism in Schrodinger Eqn. (1) | 2010.09.20 |
| 어는점내림 상수 구하기, 보론 (0) | 2010.09.03 |
 thesis.pdf
thesis.pdf