2011. 1. 29. 13:37 Mathematics/Quiz
간단한 논리학 퀴즈
각종 난감한 머리쓰는 문제를 내던 선임들을 한방에 잠재운 문제. 조금은 유명할 것 같은데...
'Mathematics > Quiz' 카테고리의 다른 글
| 기하 퀴즈 하나 (2) | 2010.04.30 |
|---|---|
| 월급을 황금 막대기로 주기 (4) | 2010.03.08 |
2011. 1. 29. 13:37 Mathematics/Quiz
| 기하 퀴즈 하나 (2) | 2010.04.30 |
|---|---|
| 월급을 황금 막대기로 주기 (4) | 2010.03.08 |
2011. 1. 16. 17:40 Mathematics
\text{To find the maximum of }G=G(x_1,\cdots,x_n)\\\text{Find }(\chi_1,\cdots,\chi_n) \text{ where } \nabla G=0\text{But }R=R(x_1,\cdots,x_n)\text{must satisfy the relation }R=0\text{To handle the problem, let }n=2\\\text{The exact differential of }R \text{ becomes}\\dR=\frac{\partial R}{\partial x_1}dx_1+\frac{\partial R}{\partial x_2}dx_2\\\text{when infinitesimal movement does not violate the requirement;}\\dR=0\text{When the function }G\text{ takes the extremum at the point}\\\text{The exact differential of }G \text{ also satisfies}\\dG=\frac{\partial G}{\partial x_1}dx_1+\frac{\partial G}{\partial x_2}dx_2=0\\\text{under the condition that }dR=0
\frac{\partial R}{\partial x_1}dx_1+\frac{\partial R}{\partial x_2}dx_2=0\\\therefore dx_1=-\frac{\frac{\partial R}{\partial x_2}}{\frac{\partial R}{\partial x_1}}dx_2\\\therefore dG=\frac{\partial G}{\partial x_1}dx_1+\frac{\partial G}{\partial x_2}dx_2\\=\left[-\frac{\partial G}{\partial x_1}\frac{\frac{\partial R}{\partial x_2}}{\frac{\partial R}{\partial x_1}}+\frac{\partial G}{\partial x_2}\right]dx_2\\=0\\\text{However, we are free to choose } dx_2 \text{, which implies}\\-\frac{\partial G}{\partial x_1}\frac{\frac{\partial R}{\partial x_2}}{\frac{\partial R}{\partial x_1}}+\frac{\partial G}{\partial x_2}=0
dR=0, dG=0\\\therefore dR-\alpha dG\\=\left[\frac{\partial R}{\partial x_1}-\alpha\frac{\partial G}{\partial x_1}\right]dx_1\\+\left[\frac{\partial R}{\partial x_2}-\alpha\frac{\partial G}{\partial x_2}\right]dx_2\\=0\text{However, as the restriction is still not removed,}\\\frac{\partial R}{\partial x_1}dx_1+\frac{\partial R}{\partial x_2}dx_2=0\\\therefore dx_1=-\frac{\frac{\partial R}{\partial x_2}}{\frac{\partial R}{\partial x_1}}dx_2
\text{Therefore under this restriction, we can freely choose }dx_2\\\frac{\partial R}{\partial x_1}dx_1+\frac{\partial R}{\partial x_2}dx_2=0
\text{Assume we choose }\alpha\text{ so that}\\\frac{\partial R}{\partial x_1}-\alpha\frac{\partial G}{\partial x_1}=0\\\text{Then }dR-\alpha dG =0 \text{ reduces to}\\\left[\frac{\partial R}{\partial x_2}-\alpha\frac{\partial G}{\partial x_2}\right]dx_2=0\\\text{As we are free to choose }dx_2 \text{, we must conclude that}\\\frac{\partial R}{\partial x_2}-\alpha\frac{\partial G}{\partial x_2}\text{ must be zero as well}
| 개드립의 마지막 정리 (0) | 2013.10.29 |
|---|---|
| 델타 분포 만들기 (6) | 2012.08.23 |
| 경계조건의 중요성 - Boundary condition (2) | 2010.08.21 |
| Involute 곡선 (10) | 2010.05.01 |
| 수학의 아름다움 (2) | 2010.04.24 |
2010. 8. 21. 13:00 Mathematics
\nabla^2\theta can be zero everywhere inside the lump of metal is for \theta to be a constant. [...]f(x,y)=e^y\cos x\\\nabla^2f=\left(\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}\right)f=0\theta(\rho,\phi,z)= J_1(\rho)\cos\phi\cosh z\theta는 상태함수의 위상이라 그 절대적인 값은 의미가 없어 임의의 지점에 임의의 값을 대응시켜 주는 것은 자유롭지만 문제는 그 자유도는 한 점에 국한된다는 것이다. 다시 한번 말하면, 금속 표면의 한 점에서 위상을 0으로 주었다고 금속 표면 전체의 위상이 0이라는 근거는 없다. 나는 파인만씨가 다음 식(21.19)만 만족하면 되기에 게이지 자유도(gauge freedom)를 이용해 \theta를 벡터포텐셜 A로 흡수시켰다고 추측할 뿐이다.mv=\hbar\nabla\theta-q\bold A~~~~~~~~\text{(21.19)}| 델타 분포 만들기 (6) | 2012.08.23 |
|---|---|
| Lagrange Multipliers - 라그랑주 승수법 (7) | 2011.01.16 |
| Involute 곡선 (10) | 2010.05.01 |
| 수학의 아름다움 (2) | 2010.04.24 |
| Power set, again (0) | 2010.04.17 |
2010. 5. 1. 23:13 Mathematics
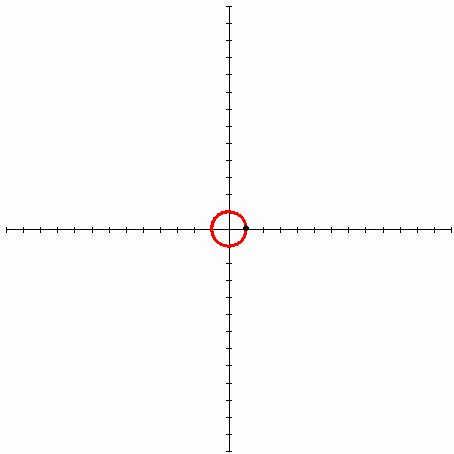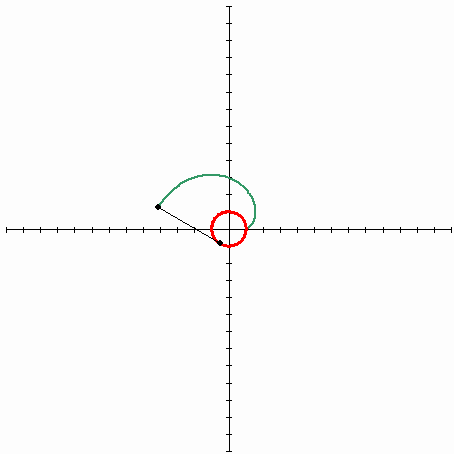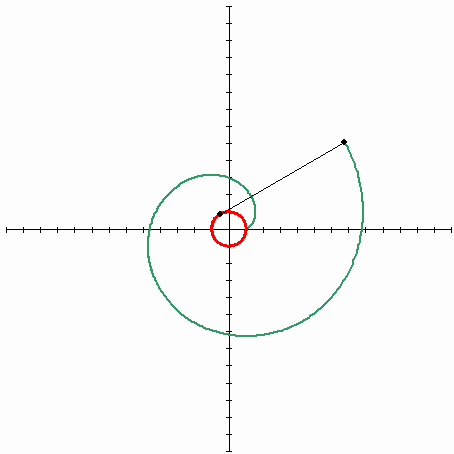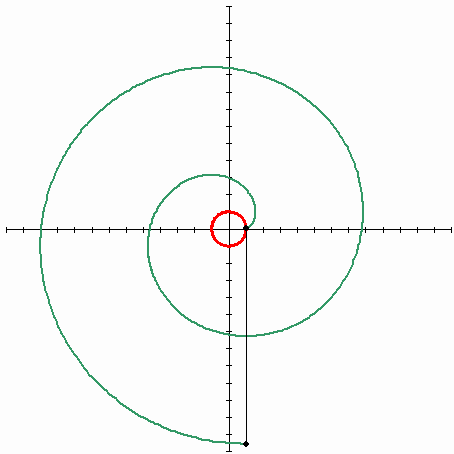
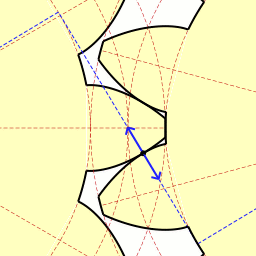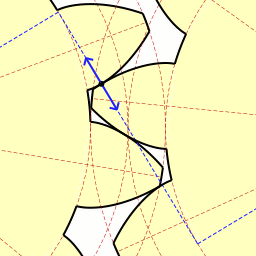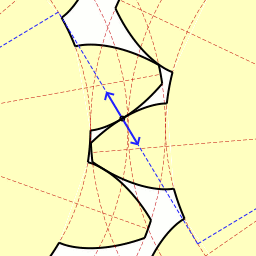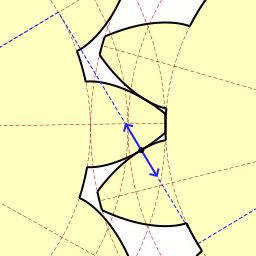
| Lagrange Multipliers - 라그랑주 승수법 (7) | 2011.01.16 |
|---|---|
| 경계조건의 중요성 - Boundary condition (2) | 2010.08.21 |
| 수학의 아름다움 (2) | 2010.04.24 |
| Power set, again (0) | 2010.04.17 |
| 무한대와 무한대가 만났을 때 (4) | 2010.04.13 |
2010. 4. 30. 02:10 Mathematics/Quiz
| 간단한 논리학 퀴즈 (5) | 2011.01.29 |
|---|---|
| 월급을 황금 막대기로 주기 (4) | 2010.03.08 |
2010. 4. 24. 16:00 Mathematics
| 경계조건의 중요성 - Boundary condition (2) | 2010.08.21 |
|---|---|
| Involute 곡선 (10) | 2010.05.01 |
| Power set, again (0) | 2010.04.17 |
| 무한대와 무한대가 만났을 때 (4) | 2010.04.13 |
| Power Set에 대한 잡담 (10) | 2010.03.15 |
2010. 4. 17. 17:34 Mathematics
| Involute 곡선 (10) | 2010.05.01 |
|---|---|
| 수학의 아름다움 (2) | 2010.04.24 |
| 무한대와 무한대가 만났을 때 (4) | 2010.04.13 |
| Power Set에 대한 잡담 (10) | 2010.03.15 |
| 야코비 행렬(Jacobian matrix) (12) | 2010.02.24 |
2010. 4. 13. 01:19 Mathematics
| 수학의 아름다움 (2) | 2010.04.24 |
|---|---|
| Power set, again (0) | 2010.04.17 |
| Power Set에 대한 잡담 (10) | 2010.03.15 |
| 야코비 행렬(Jacobian matrix) (12) | 2010.02.24 |
| 선형대수와 행렬 (0) | 2010.02.04 |
2010. 3. 15. 23:14 Mathematics
| Power set, again (0) | 2010.04.17 |
|---|---|
| 무한대와 무한대가 만났을 때 (4) | 2010.04.13 |
| 야코비 행렬(Jacobian matrix) (12) | 2010.02.24 |
| 선형대수와 행렬 (0) | 2010.02.04 |
| 루빅스로 배우는 군론 (0) | 2010.01.27 |
2010. 3. 8. 22:39 Mathematics/Quiz
| 간단한 논리학 퀴즈 (5) | 2011.01.29 |
|---|---|
| 기하 퀴즈 하나 (2) | 2010.04.30 |
2010. 2. 24. 23:47 Mathematics


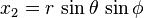

![J_F(r,\theta,\phi) =\begin{bmatrix}
\dfrac{\partial x_1}{\partial r} & \dfrac{\partial x_1}{\partial \theta} & \dfrac{\partial x_1}{\partial \phi} \\[3pt]
\dfrac{\partial x_2}{\partial r} & \dfrac{\partial x_2}{\partial \theta} & \dfrac{\partial x_2}{\partial \phi} \\[3pt]
\dfrac{\partial x_3}{\partial r} & \dfrac{\partial x_3}{\partial \theta} & \dfrac{\partial x_3}{\partial \phi} \\
\end{bmatrix}=\begin{bmatrix}
\sin\theta\, \cos\phi & r\, \cos\theta\, \cos\phi & -r\, \sin\theta\, \sin\phi \\
\sin\theta\, \sin\phi & r\, \cos\theta\, \sin\phi & r\, \sin\theta\, \cos\phi \\
\cos\theta & -r\, \sin\theta & 0
\end{bmatrix}.](http://upload.wikimedia.org/math/d/7/9/d791528200a6f3c81162837ca9624f39.png)
| 무한대와 무한대가 만났을 때 (4) | 2010.04.13 |
|---|---|
| Power Set에 대한 잡담 (10) | 2010.03.15 |
| 선형대수와 행렬 (0) | 2010.02.04 |
| 루빅스로 배우는 군론 (0) | 2010.01.27 |
| 무한대의 비교: 자연수와 실수 (0) | 2010.01.13 |
2010. 2. 4. 00:56 Mathematics
| Power Set에 대한 잡담 (10) | 2010.03.15 |
|---|---|
| 야코비 행렬(Jacobian matrix) (12) | 2010.02.24 |
| 루빅스로 배우는 군론 (0) | 2010.01.27 |
| 무한대의 비교: 자연수와 실수 (0) | 2010.01.13 |
| Laplace 변환을 이용한 미분방정식 풀이 (2) | 2009.12.17 |
2010. 1. 27. 13:20 Mathematics
| 야코비 행렬(Jacobian matrix) (12) | 2010.02.24 |
|---|---|
| 선형대수와 행렬 (0) | 2010.02.04 |
| 무한대의 비교: 자연수와 실수 (0) | 2010.01.13 |
| Laplace 변환을 이용한 미분방정식 풀이 (2) | 2009.12.17 |
| 각종 변환들 (0) | 2009.12.15 |
2010. 1. 13. 15:27 Mathematics

| 선형대수와 행렬 (0) | 2010.02.04 |
|---|---|
| 루빅스로 배우는 군론 (0) | 2010.01.27 |
| Laplace 변환을 이용한 미분방정식 풀이 (2) | 2009.12.17 |
| 각종 변환들 (0) | 2009.12.15 |
| Fourier 변환의 고유함수 (0) | 2009.12.15 |
2009. 12. 17. 01:02 Mathematics
| 루빅스로 배우는 군론 (0) | 2010.01.27 |
|---|---|
| 무한대의 비교: 자연수와 실수 (0) | 2010.01.13 |
| 각종 변환들 (0) | 2009.12.15 |
| Fourier 변환의 고유함수 (0) | 2009.12.15 |
| 적분놀이 (0) | 2009.12.05 |
2009. 12. 15. 19:36 Mathematics


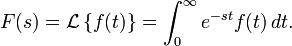
| 무한대의 비교: 자연수와 실수 (0) | 2010.01.13 |
|---|---|
| Laplace 변환을 이용한 미분방정식 풀이 (2) | 2009.12.17 |
| Fourier 변환의 고유함수 (0) | 2009.12.15 |
| 적분놀이 (0) | 2009.12.05 |
| Tensor(1) (2) | 2009.10.16 |
2009. 12. 15. 19:08 Mathematics
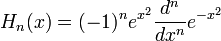
| 무한대의 비교: 자연수와 실수 (0) | 2010.01.13 |
|---|---|
| Laplace 변환을 이용한 미분방정식 풀이 (2) | 2009.12.17 |
| 각종 변환들 (0) | 2009.12.15 |
| 적분놀이 (0) | 2009.12.05 |
| Tensor(1) (2) | 2009.10.16 |
2009. 12. 5. 01:04 Mathematics
| 무한대의 비교: 자연수와 실수 (0) | 2010.01.13 |
|---|---|
| Laplace 변환을 이용한 미분방정식 풀이 (2) | 2009.12.17 |
| 각종 변환들 (0) | 2009.12.15 |
| Fourier 변환의 고유함수 (0) | 2009.12.15 |
| Tensor(1) (2) | 2009.10.16 |
2009. 10. 16. 01:00 Mathematics
![R(\theta) = \begin{bmatrix}
\cos \theta & -\sin \theta \\[3pt]
\sin \theta & \cos \theta \\
\end{bmatrix}\quad(\text{counterclockwise rotation by }\theta).](http://upload.wikimedia.org/math/2/1/2/212f5d8ef74b4a7ca1506ae96b96fbcd.png)
T_{x'y'}=p^x_{x'} p^x_{y'} T_{xx} + p^x_{x'} p^y_{y'} T_{xy} + p^y_{x'} p^x_{y'} T_{yx} + p^y_{x'} p^y_{y'} T_{yy}

| 무한대의 비교: 자연수와 실수 (0) | 2010.01.13 |
|---|---|
| Laplace 변환을 이용한 미분방정식 풀이 (2) | 2009.12.17 |
| 각종 변환들 (0) | 2009.12.15 |
| Fourier 변환의 고유함수 (0) | 2009.12.15 |
| 적분놀이 (0) | 2009.12.05 |